Correct way to numerically calculate a sum-CodePudding

I am trying to numerically calculate a sum:

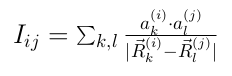
The sum formula

I fully understand that it is an easy sum, however, my mind keeps tingling me for a few days consequently, if I am doing it correctly.

Here is an outline of a C code that I have written to calculate it:

struct vecs{
    float x;
    float y;
    float z;
    float a;
};

struct vector_file{
    int id;
    vector<vecs> VAL;
};

vector<vector_file> VEC;

I[10][10]={}

double absolute_val(double xi, double yi, double zi, double xj, double yj, double zj){
    return(sqrt(pow(xi-xj,2) pow(yi-yj,2) pow(zi-zj,2)));
}

for (int i=0;i<VEC.size();i  ){
        for (int j=0;j<i;j  ){
            double integ=0;
                for (int k=0;k<VEC[i].VAL.size();k  ){
                    for (int l=0;l<VEC[j].VAL.size();l  ){
                        integ =VEC[i].VAL[k].a*VEC[j].VAL[l].a/absolute_val(VEC[i].VAL[k].x,VEC[i].VAL[k].y,VEC[i].VAL[k].z,VEC[j].VAL[l].x,VEC[j].VAL[l].y, VEC[j].VAL[l].z);
                    }
                }
            I[i][j]=integ;
        }
    }

I only need the off-diagonal elements and do not need the upper triangular part of the matrix as it is analogous to lower triangular part. I have checked it multiple times, however, still going back and wondering, if I have done it correctly.

Thank you so much in advance for taking time to look at it.

CodePudding user response：

Yes, your code is correct. If you want to make it "more obviously" correct, I would move it closer to the mathematical definitions by defining some helper functions.

Concretely:

const vecs& R(int upper, int lower) { return VEC[upper].VAL[lower]; }
const float a(int upper, int lower) { return VEC[upper].VAL[lower].a; }
int num_vecs(int upper) { return VEC[upper].VAL.size(); }

Next, I would write magnitude_diff to accept two vecs. It is not strictly the magnitude because you're only looking at three of the four components, but I don't feel comfortable defining operator - for 3/4 components either.

double magnitude_diff(const vecs& i, const vecs& j){
    return sqrt(pow(i.x-j.x,2)   pow(i.y-j.y,2)   pow(i.z-j.z,2));
}

and then your inner loop stays very close to the formula:

double integ=0;
for (int k=0; k < num_vecs(i); k  ){
  for (int l=0; l < num_vecs(j); l  ){
    integ  = a(i, k) * a(j, l) / magnitude_diff(R(i, k), R(j, l));                                        
  }
}
I[i][j] = integ;