4D chaotic system Lyapunov exponent-CodePudding

I am trying to work on the 4 dimensional chaotic attractor Lyapunov spectrum and there values so far the code mention below works well for three dimensional system but errors arise in 4D and 5D system

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint

def diff_Lorenz(u):
    x,y,z,w= u
    f = [a*(y-x) , x*z w, b-x*y, z*y-c*w]
    Df = [[-a,a,0,0], [z,0, x,1], [-y, -x, 0,0],[0,z,y,-c]]
    return np.array(f), np.array(Df)


def LEC_system(u):
    #x,y,z = u[:3]
    U = u[2:18].reshape([4,4])
    L = u[12:15]
    f,Df = diff_Lorenz(u[:4])
    A = U.T.dot(Df.dot(U))
    dL = np.diag(A).copy();
    for i in range(4):
        A[i,i] = 0
        for j in range(i 1,4): A[i,j] = -A[j,i]
    dU = U.dot(A)
    return np.concatenate([f,dU.flatten(),dL])


a=6;b=11;c=5;

u0 = np.ones(4)
U0 = np.identity(4)
L0 = np.zeros(4)
u0 = np.concatenate([u0, U0.flatten(), L0])
t = np.linspace(0,10,301)
u = odeint(lambda u,t:LEC_system(u),u0,t, hmax=0.05)
L = u[5:,12:15].T/t[5:]

# plt.plot(t[5:],L.T) 
# plt.show()
p1=L[0,:];p2=L[1,:];p3=L[2,:];p4=L[3,:]
L1 = np.mean(L[0,:]);L2=np.average(L[1,:]);L3=np.average(L[2,:]);L4=np.average(L[3,:])
t1 = np.linspace(0,100,len(p1))
plt.plot(t1,p1);plt.plot(t1,p2);plt.plot(t1,p3);plt.plot(t1,p4)

# plt.show()
print('LES= ',L1,L2,L3,L4)

the output error is

D:\anaconda3\lib\site-packages\scipy\integrate\odepack.py:247: ODEintWarning: Excess work done on this call (perhaps wrong Dfun type). Run with full_output = 1 to get quantitative information.
  warnings.warn(warning_msg, ODEintWarning)
---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
~\AppData\Local\Temp/ipykernel_7008/1971199288.py in <module>
     32 # plt.plot(t[5:],L.T)
     33 # plt.show()
---> 34 p1=L[0,:];p2=L[1,:];p3=L[2,:];p4=L[3,:]
     35 L1=np.mean(L[0,:]);L2=np.average(L[1,:]);L3=np.average(L[2,:]);L4=np.average(L[3,:])
     36 t1 = np.linspace(0,100,len(p1))

IndexError: index 3 is out of bounds for axis 0 with size 3

what is wrong?

output expected is L1=.5162,L2=-.0001,L3=-4.9208,L4=-6.5954

CodePudding user response：

In LEC_system(u), the flat vector u contains in sequence

the state vector, n components,
the eigenbasis U, a n x n matrix
the accumulated exponents L, n components.

With n=4, this translates thus to the decomposition

def LEC_system(u):
    #x,y,z,w = u[:4]
    U = u[4:20].reshape([4,4])
    L = u[20:24]
    f,Df = diff_Lorenz(u[:4])
    A = U.T.dot(Df.dot(U))
    dL = np.diag(A).copy();
    for i in range(4):
        A[i,i] = 0
        for j in range(i 1,4): A[i,j] = -A[j,i]
    dU = U.dot(A)
    return np.concatenate([f,dU.flatten(),dL])

Of course, in the evaluation after the integration one has to likewise use the correct segment of the state vector

L = u[5:,20:24].T/t[5:]

Then I get the plot

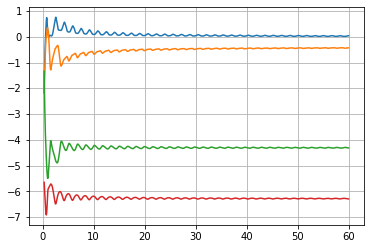
and only using the latter quart of the graphs, after integrating to t=60

LES=  0.029214865425355396 -0.43816854013111833 -4.309199339754925 -6.28183676249535

This still are not the expected values, as that appears to be contracting along all directions transversal to the solution curve.