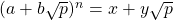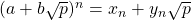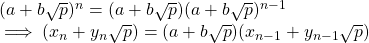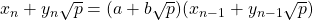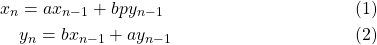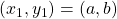I want to write a function in python called compute(a,b,p,n) where a,b,n are integers and n>0, that outputs the tuple (x,y) (x,y being integers) such that

Note that the constraints of the problem state that you're not allowed to use any internal libraries.

Now, I set about to solve this problem by writing a recursive function. To that end, let us assume that

But, we also have

Therefore, we have

Equating coefficients now yields

With

Now, making use of the equations in (1) and (2), we can write a simple and straightforward recursive python function as

def compute(a,b,p,n):
    
     if n==1:
        return  (1,1)

     if n>1:
        return (a*compute(a,b,p,n-1)[0] b*p*compute(a,b,p,n-1)[1], b*compute(a,b,p,n-1)[0] a*compute(a,b,p,n-1)[1])

This code works fine for small values of n, say upto 10, but for large values of n it is horribly inefficient. Is there some alternate way to approach this problem which works faster, or perhaps some way to optimize this code so that it runs faster?

CodePudding user response：

The first optimization possibility is to only run compute(a,b,p,n-1) once per recursive call. then you would have

def compute(a,b,p,n):
    
     if n==1:
        return  (1,1)

     if n>1:
        recursive_compute = compute(a,b,p,n-1)
        return (a*recursive_compute[0] b*p*recursive_compute[1], b*recursive_compute[0] a*recursive_compute[1])

The second thing you could do is to drop recursion and iterate from 1 to n instead of from n to 1. Recursion in python is not tail call optimized, so your memory usage will increase after each recursive call.

This is one approach

def compute(a,b,p,n):
    current = (1,1)
    for _ in range(n -1):
        current = (a*current[0] b*p*current[1], b*current[0] a*current[1])
    return current

Since we don't grow the stack with recursion and don't allocate, this should be fast enough

CodePudding user response：

A nice recursive solution for raising base B to the n^th power is to leverage the identities Bⁿ = (B²)^n/2 for n even, or B*(B²)^n/2 for n odd. This results in an algorithm with O(log n) computational complexity, yielding a significant improvement for large values of n. For your particular problem, B = (a b*sqrt(p)). Carrying out the corresponding multiplications for both even and odd terms and implementing in python gives the following:

def compute(a,b,p,n):
    if n == 1: return (a,b)
    c, d = compute(a*a   b*b*p, 2*a*b, p, n // 2)
    if n % 2 == 0:
        return (c, d)
    else:
        return (a*c   b*d*p, a*d   b*c)

In implementing this I noticed that your base case is incorrect. Since the problem specification says that n is strictly greater than 0, the base case should be (a,b) for n == 1. If you want to include zero as a possible power, it would become (1,0) for n == 0. You can confirm that this is correct by making that change to your code and comparing the results to a hand-calculation of compute(1, 2, 9, 2), i.e., a simple square of (1 2sqrt(9))² = 49 should be (37 4sqrt(9)) = 49. Your code currently produces (19 3sqrt(9)) = 28 but yields the correct answer when the base case is corrected as above.

Another advantage of this divide and conquer approach relative to your recursion is that it can handle very large values of n without stack overflowing.

CodePudding user response：

Happily, your equations are linear:

x_n = a x_(n-1)   b p x_(n-1)
y_n = b x_(n-1)     a y_(n-1)

Let us rewrite these two scalar equations as a single matrix-vector equation:

X_n = M X_(n-1)

with:
  X_n = (x_n)    M = (a  bp)
        (y_n)        (b  a )

This recursive equation gives us a direct equation for X_n as a function of n:

X_n = M^(n-1) X_1

where ^ means "matrix exponentiation".

Now, if you had access to an external library, you could use that library's fast matrix exponentiation function. But since you don't, you'll have to write it yourself!

Fast matrix exponentiation is basically the same as fast scalar exponentiation: instead of multiplying M by itself n times, we're going to use the fact that M^(2k) = (M^k)^2 to cut down sharply on the number of matrix multiplications.

We end up with the following code:

def matmul(A, B):
    return [[sum(A[j][i] * B[k][j] for j in range(2)) for i in range(2)] for k in range(2)]

def matvecmul(M, X):
    return [M[0][0]*X[0]   M[0][1]*X[1], M[1][0]*X[0]   M[1][1]*X[1]]

def matpow(M, n):
    if n == 1:
        return M
    elif n % 2 == 0:
        S = matpow(M, n//2)
        return matmul(S, S)
    else:
        S = matpow(M, n//2)
        return matmul(M, matmul(S, S))

def compute(a, b, p, n):
    Mn = matpow([[a, b*p], [b, a]], n-1)
    return matvecmul(Mn, [a,b])

Testing:

>>> from math import sqrt
>>> import timeit
>>> start = timeit.default_timer(); x,y = compute(sqrt(2)/2, sqrt(2)/2, -1, 100000); stop = timeit.default_timer()
>>> stop - start       # execution time in seconds
0.00040509300015401095 # 0.4 millisecond
>>> x,y                # should be (1, 0) because (sqrt(2)/2 * (1   sqrt(-1))) ** 100000 == exp(i pi/4)**(8*12500) == exp(i 2pi) == 1
(1.0000000000073506, 0.0)