I have two normalized angles (in the range of 0 to 360 degrees) and want to compare them using a score from 0 to 1.

For example:

var angle1 = 90;
var angle2 = 100;

// Something like this, but with respect to the direction the angles pointing to

var score = 0.9;

I came up with the following code:

function modulo(x, y){

    return (x % y   y) % y;

}

// Calculates the closest distance between the two angles

var relativeAngle = angle2 - angle1;
relativeAngle = modulo((relativeAngle   180), 360) - 180;
  
// Converts the result to a score and logs the result
  
console.log(1 - (Math.abs(relativeAngle) / 360));

The issue I am having is that 0, 90 gives the same result as 0, 270 (0.75), which is logical but not useful for comparing the angles as they are pointing in opposite directions.

What I am looking for is a method to compare the angles with respect to the orientation using a score from 0 to 1. Does anyone have an idea how I could get this to work? Thanks in advance!

Edit 1, an example:

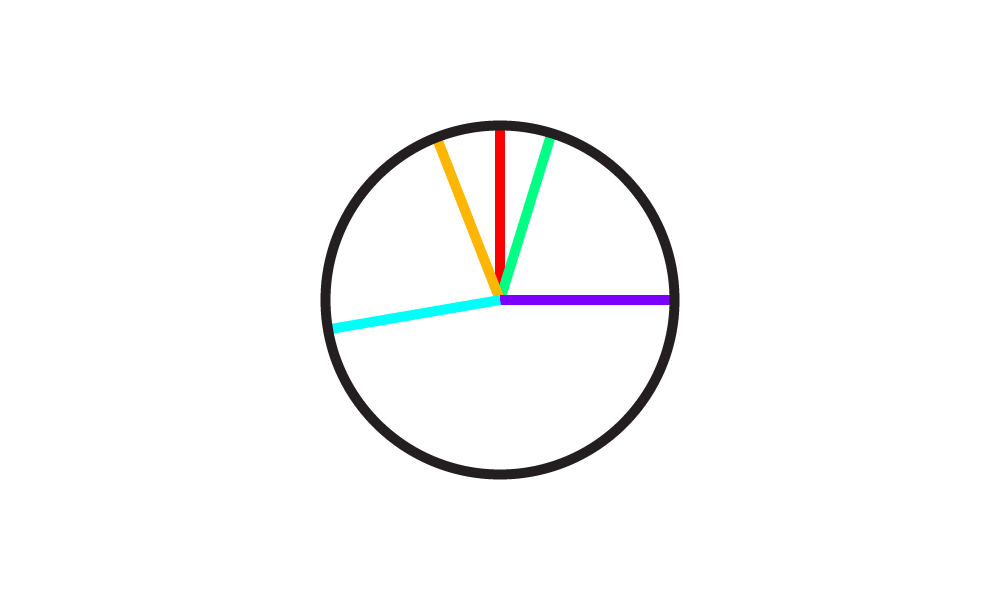
In this image the green, yellow and red angles are closer to each other, so they should have a higher similarity.

If I would guess:

red-green = 0.9 red-orange = 0.8

Purple however is about as far from blue as possible.

So the similarity should be something like:

purple-blue = 0.1

Edit 2, how the algorithm should work:

CodePudding user response：

From your description, it seems you want to somehow distill average orientation and separation together into a single value. I'm not sure that's possible due to aliasing (which you hint at in your question).

Comparing a pair of angles as you describe is simply calculating their minimum angle of separation.

However, comparing two sets of angles in the way you describe also needs to take into account the difference in the relative orientation between the two sets. Since each pair could be converted to a [separation, orientation] pair, two pairs could be scored relatively based on Cartesian distance.

// Smallest difference between angles as on a circle
// range [0, 1)
const angle = (a,b) => {
  const results = a > b ? a - b : b - a;
  return (results > 180 ? 360 - results : results) / 180;
}

// Midway between two angles as on a circle
// range [0, 1)
const direction = (a,b) => {
  const large = (a > b ? a - b : b - a) > 180;
  const results = (a   b) / 2;
  return (results   (large ? (results >= 180 ? -180 : 180 ) : 0)) / 180;
};

// Cartesian distance score
// range [0, 1)
// x is angle, y is direction
const distance = (x0, y0, x1, y1) => {
  // direction wraps around so account for that
  if((y0 > y1 ? y0 - y1 : y1 - y0) > 0.5) y0  = 1;

  // the `*2` is because the wrap-around distance is never more than half the interval. 
  return Math.sqrt((x0-x1)**2   ((y0-y1)*2)**2) / Math.SQRT2;
}

// Difference score for two angles, a and b
const diff = (a,b) => angle(a, b);

// Difference score for two pairs of angles [[a0, b0], [a1, b1]]
const diff2 = (a0, b0, a1, b1) => distance(
  angle(a0, b0), direction(a0, b0),
  angle(a1, b1), direction(a1, b1)
);