Pair two 1D arrays by their value and index-CodePudding

I have two 1D arrays of the same length as this:

import numpy as np

a = np.array([1, 1, 1, 2, 2, 3, 4,  5])
b = np.array([7, 7, 8, 8, 9, 8, 10, 10])

The value of a is increasing while b is random.

I wanna pair them by their values following the steps below:

Pick the first unique value ([1]) of array a and get the unique numbers ([7, 8]) of array b at the same index.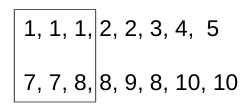
If some paired numbers ([8]) appear again in b, then pick the number at the same index of a.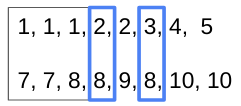
Then, some new paired number ([2]) which appears again in a, the numbers in b at the same index are selected.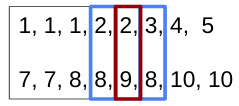

Finally, the result should be:

[1, 2, 3] is paired with [7, 8, 9]

[4, 5] is paired with [10]

CodePudding user response：

I tried doing this by iterating both the arrays simultaneously and keeping track of what element is associated with which index of the result. Let me know if this works for you?

a = [1, 1, 1, 2, 2, 3, 4,  5]
b = [7, 7, 8, 8, 9, 8, 10, 10]

tracker_a = dict()
tracker_b = dict()

result = []
index = 0
for elem_a, elem_b in zip(a, b):
  if elem_a in tracker_a:
    result[tracker_a[elem_a]][1].add(elem_b)
    tracker_b[elem_b] = tracker_a[elem_a] 
  elif elem_b in tracker_b:
    result[tracker_b[elem_b]][0].add(elem_a)
    tracker_a[elem_a] = tracker_b[elem_b]
  else:
    tracker_a[elem_a] = index
    tracker_b[elem_b] = index
    result.append([{elem_a}, {elem_b}])
    index  = 1
    
print(result)

Output:

[[{1, 2, 3}, {8, 9, 7}], [{4, 5}, {10}]]

Complexity: O(n)

CodePudding user response：

It looks like there is no easy way for a vectorised (no looping) solution since it's a graph theory problem of finding connected components. If you still want to have a performant script that works fast on big data, you could use igraph library which is written in C.

TL;DR

I assume your input corresponds to edges of some graph:

>>> np.transpose([a, b])
array([[ 1,  7],
       [ 1,  7],
       [ 1,  8],
       [ 2,  8],
       [ 2,  9],
       [ 3,  8],
       [ 4, 10],
       [ 5, 10]])

So your vertices are:

>>> np.unique(np.transpose([a, b]))
array([ 1,  2,  3,  4,  5,  7,  8,  9, 10])

And you would be quite happy (at least at the beginning) to recognise communities, like:

tags = np.transpose([a, b, communities])
>>> tags
    array([[ 1,  7,  0],
           [ 1,  7,  0],
           [ 1,  8,  0],
           [ 2,  8,  0],
           [ 2,  9,  0],
           [ 3,  8,  0],
           [ 4, 10,  1],
           [ 5, 10,  1]])

so that you have vertices (1, 2, 3, 7, 8, 9) included in community number 0 and vertices (4, 5, 10) included in community number 1.

Unfortunately, igraph doesn't support labeling graph nodes from 1 to 10 or any gaps of ids in labels. It must start from 0 and have no gaps in ids. So you need to store initial indices and after that relabel vertices so that edges are:

vertices_old, inv = np.unique(np.transpose([a,b]), return_inverse=True)
edges_new = inv.reshape(-1, 2)
>>> vertices_old
array([ 1,  2,  3,  4,  5,  7,  8,  9, 10]) #new ones are: [0, 1, 2, ..., 8]
>>> edges_new
array([[0, 5],
       [0, 5],
       [0, 6],
       [1, 6],
       [1, 7],
       [2, 6],
       [3, 8],
       [4, 8]], dtype=int64)

The next step is to find communities using igraph (pip install python-igraph). You can run the following:

import igraph as ig
graph = ig.Graph(edges = edges_new)
communities = graph.clusters().membership #type: list
communities = np.array(communities)
>>> communities
array([0, 0, 0, 1, 1, 0, 0, 0, 1]) #tags of nodes [1 2 3 4 5 7 8 9 10]

And then retrieve tags of source vertices (as well as tags of target vertices):

>>> communities = communities[edges_new[:, 0]] #or [:, 1]
array([0, 0, 0, 0, 0, 0, 1, 1])

After you find communities, the second part of solution appears to be a typical groupby problem. You can do it in pandas:

import pandas as pd
def get_part(source, communities):
    part_edges = np.transpose([source, communities])
    part_idx = pd.DataFrame(part_edges).groupby([1]).indices.values() #might contain duplicated source values
    part = [np.unique(source[idx]) for idx in part1_idx]
    return part
>>> get_part(a, communities), get_part(b, communities)
([array([1, 2, 3]), array([4, 5])], [array([7, 8, 9]), array([10])])

Final Code

import igraph as ig
import numpy as np
import pandas as pd

def get_part(source, communities):
    '''find set of nodes for each community'''
    part_edges = np.transpose([source, communities])
    part_idx = pd.DataFrame(part_edges).groupby([1]).indices.values() #might contain duplicated source values
    part = [np.unique(source[idx]) for idx in part1_idx]
    return part

a = np.array([1, 1, 1, 2, 2, 3, 4,  5])
b = np.array([7, 7, 8, 8, 9, 8, 10, 10])

vertices_old, inv = np.unique(np.transpose([a,b]), return_inverse=True)
edges_new = inv.reshape(-1, 2)
graph = ig.Graph(edges = edges_new)
communities = np.array(graph.clusters().membership)
communities = communities[edges_new[:,0]] #or communities[edges_new[:,1]]
>>> get_part(a, communities), get_part(b, communities)
([array([1, 2, 3]), array([4, 5])], [array([7, 8, 9]), array([10])])