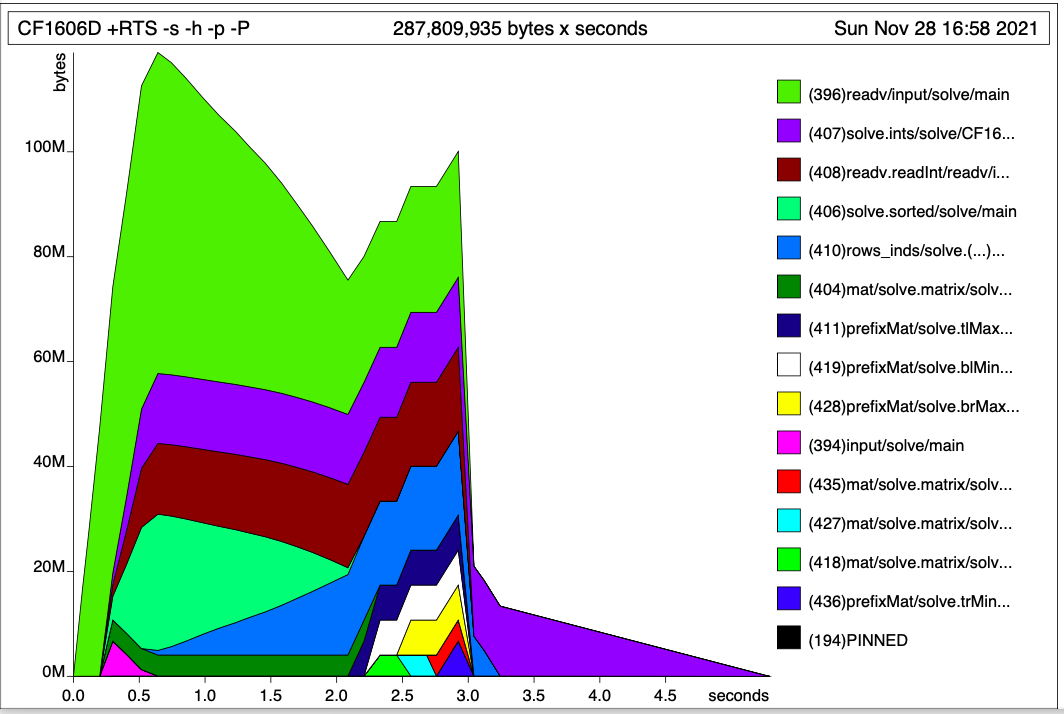
Functions readv and readv.readInt, responsible for parsing integers and saving them into a 2D list, are taking around 50-70 MB, as opposed to around 16 MB = (10⁶ integers) × (8 bytes per integer 8 bytes per link).

Is there a hope I can get the total memory below 256 MB? I'm already using Text package for input. Maybe I should avoid lists altogether and directly read integers from stdin to the array. How can we do that? Or, is the issue elsewhere?

Code

{-# OPTIONS_GHC -O2 #-}
module CF1606D where
import qualified Data.Text as T
import qualified Data.Text.IO as TI
import qualified Data.Text.Read as TR
import Control.Monad
import qualified Data.List as DL
import qualified Data.IntSet as DS
import Control.Monad.ST
import Data.Array.ST.Safe
import Data.Int (Int32)
import Data.Array.Unboxed

solve :: IO ()
solve =  do
  ~[n,m] <- readv      
  -- 2D list
  input <- {-# SCC input #-} replicateM (fromIntegral n) readv     
  let
      ints = [1..]
      sorted = DL.sortOn (head.fst) (zip input ints)
      (rows,indices) = {-# SCC rows_inds #-} unzip sorted    
      -- 2D list converted into matrix:
      matrix = mat (fromIntegral n) (fromIntegral m) rows           
      infinite = 10^7
      asc x y = [x,x 1..y]
      desc x y = [y,y-1..x]    
      -- Four prefix-matrices:
      tlMax = runSTUArray $ prefixMat max 0 asc asc (subtract 1) (subtract 1) =<< matrix
      blMin = runSTUArray $ prefixMat min infinite desc asc ( 1) (subtract 1) =<< matrix
      trMin = runSTUArray $ prefixMat min infinite asc desc (subtract 1) ( 1) =<< matrix
      brMax = runSTUArray $ prefixMat max 0 desc desc ( 1) ( 1) =<< matrix    
      good _ (i,j)
        | tlMax!(i,j) < blMin!(i 1,j) && brMax!(i 1,j 1) < trMin!(i,j 1) = Left (i,j)
        | otherwise = Right ()
      {-# INLINABLE good #-}
      nearAns = foldM good () [(i,j)|i<-[1..n-1],j<-[1..m-1]]
      ans = either (\(i,j)-> "YES\n"    color n (take i indices)    " "    show j) (const "NO") nearAns
  putStrLn ans

type I = Int32
type S s = (STUArray s (Int, Int) I)
type R = Int -> Int -> [Int]
type F = Int -> Int

mat :: Int -> Int -> [[I]] -> ST s (S s)
mat n m rows = newListArray ((1,1),(n,m)) $ concat rows

prefixMat :: (I->I->I) -> I -> R -> R -> F -> F -> S s -> ST s (S s)
prefixMat opt worst ordi ordj previ prevj mat = do
  ((ilo,jlo),(ihi,jhi)) <- getBounds mat
  pre <- newArray ((ilo-1,jlo-1),(ihi 1,jhi 1)) worst
  forM_ (ordi ilo ihi) $ \i-> do
    forM_ (ordj jlo jhi) $ \j -> do
      matij <- readArray mat (i,j)
      prei <- readArray pre (previ i,j)
      prej <- readArray pre (i, prevj j)
      writeArray pre (i,j) (opt (opt prei prej) matij)
  return pre

color :: Int -> [Int] -> String
color n inds = let
  temp = DS.fromList inds
  colors = [if DS.member i temp then 'B' else 'R' | i<-[1..n]]
  in colors

readv :: Integral t => IO [t]
readv = map readInt . T.words <$> TI.getLine where
  readInt = fromIntegral . either (const 0) fst . TR.signed TR.decimal
{-# INLINABLE readv #-}

main :: IO ()
main = do
  ~[n] <- readv
  replicateM_ n solve

Quick description of the code above:

Read n rows each having m integers.
Sort the rows by their first element.
Now compute four 'prefix matrices', one from each corner. For top-left and bottom-right corners, it's the prefix-maximum, and for the other two corners, it's the prefix-minimum that we need to compute.
Find a cell [i,j] at which these prefix matrices satisfy the following condition: top_left [i,j] < bottom_left [i,j] and top_right [i,j] > bottom_right [i,j]
For rows 1 through i, mark their original indices (i.e. position in the unsorted input matrix) as Blue. Mark the rest as Red.

Sample input and Commands

Sample input: inp3.txt.

Command:

> stack ghc -- -main-is CF1606D.main -with-rtsopts="-s -h -p -P" -rtsopts -prof -fprof-auto CF1606D
> gtime -v ./CF1606D < inp3.txt > outp
    ...
    ...
    MUT     time    2.990s  (  3.744s elapsed)    #    RTS -s output
    GC      time    4.525s  (  6.231s elapsed)    #    RTS -s output
    ...
    ...
    Maximum resident set size (kbytes): 408532    #    >256 MB (gtime output)

> stack exec -- hp2ps -t0.1 -e8in -c CF1606D.hp && open CF1606D.ps

Question about GC: As shown above in the RTS -s output, GC seems to be taking longer than the actual logic execution. Is this normal? Is there a way to visualize the GC activity over time? I tried making matrices strict but that didn't have any impact.

Probably this is not a functional-friendly problem at all (although I'll be happy to be disproved on this). For example, Java uses GC too but there are lots of successful Java submissions. Still, I want to see how far I can push. Thanks!

CodePudding user response：

Contrary to common belief Haskell is quite friendly with respect to problems like that. The real issue is that the array library that comes with GHC is total garbage. Another big problem is that everyone is taught in Haskell to use lists where arrays should be used instead, which is usually one of the major sources of slow code and memory bloated programs. So, it is not surprising that GC takes a long time, it is because there is way too much stuff being allocation. Here is a run on the supplied input for the solution provided below:

   1,483,547,096 bytes allocated in the heap
         566,448 bytes copied during GC
      18,703,640 bytes maximum residency (3 sample(s))
       1,223,400 bytes maximum slop
              32 MiB total memory in use (0 MB lost due to fragmentation)

                                     Tot time (elapsed)  Avg pause  Max pause
  Gen  0      1399 colls,     0 par    0.009s   0.009s     0.0000s    0.0011s
  Gen  1         3 colls,     0 par    0.002s   0.002s     0.0006s    0.0016s

  TASKS: 4 (1 bound, 3 peak workers (3 total), using -N1)

  SPARKS: 0 (0 converted, 0 overflowed, 0 dud, 0 GC'd, 0 fizzled)

  INIT    time    0.001s  (  0.001s elapsed)
  MUT     time    0.484s  (  0.517s elapsed)
  GC      time    0.011s  (  0.011s elapsed)
  EXIT    time    0.001s  (  0.002s elapsed)
  Total   time    0.496s  (  0.530s elapsed)

The solution provided below uses an array library massiv, which makes it impossible to submit to codeforces. However, hopefully the goal is to get better at Haskell, rather than get points on some website.

The red-blue matrix can be separated into two stages: read and solve

Read

Read the dimensions

In the main function we only read total number of arrays and dimensions for each array. Also we print the outcome. Nothing exciting here. (Note that the linked file inp3.txt has a larger array than the limits defined in the problem: n*m <= 10^6)

import Control.Monad.ST
import Control.Monad
import qualified Data.ByteString as BS
import Data.Massiv.Array as A hiding (B)
import Data.Massiv.Array.Mutable.Algorithms (quicksortByM_)
import Control.Scheduler (trivialScheduler_)

main :: IO ()
main = do
  t <- Prelude.read <$> getLine
  when (t < 1 || t > 1000) $ error $ "Invalid t: "    show t
  replicateM_ t $ do
    dimsStr <- getLine
    case Prelude.map Prelude.read (words dimsStr) of
      -- Test file fails this check: && n * m <= 10 ^ (6 :: Int) -> do
      [n, m] | n >= 2 && m > 0 && m <= 5 * 10 ^ (5 :: Int) -> do
        mat <- readMatrix n m
        case solve mat of
          Nothing -> putStrLn "NO"
          Just (ix, cs) -> do
            putStrLn "YES"
            putStr $ foldMap show cs
            putStr " "
            print ix
      _ -> putStrLn $ "Unexpected dimensions: "    show dimsStr

Read the array in

Loading the input into array is the major source of problems int the original question:

there is no need to rely on text, ascii characters is the only valid input expected by the problem.
input is read into a list of lists. That list of lists is the real source of the memory overhead.
Sorting lists is ridiculously slow and memory hungry.

Normally in such situation it would be much better to read input in a streaming fashion using something like conduit. In particular, reading input as stream of bytes and parsing those bytes as numbers would be the optimal solution. That being said there are hard requirements on the width of each array in the description of the problem, so we can get away with reading input line-by-line as a ByteString and then parsing numbers (assumed unsigned for simplicity) in each line and write those numbers into array at the same time. This ensures that at this stage we will only have allocated the resulting array and a single line as sequence of bytes. This could be done cleaner with a parsing library like attoparsec, but problem is simple enough to just do it adhoc.

type Val = Word

readMatrix :: Int -> Int -> IO (Matrix P Val)
readMatrix n m = createArrayS_ (Sz2 n m) readMMatrix

readMMatrix :: MMatrix RealWorld P Val -> IO ()
readMMatrix mat =
  loopM_ 0 (< n) (  1) $ \i -> do
    line <- BS.getLine
    --- ^ reads at most 10Mb because it is known that input will be at most
    -- 5*10^5 Words: 19 digits max per Word and one for space: 5*10^5 * 20bytes
    loopM 0 (< m) (  1) line $ \j bs ->
      let (word, bs') = parseWord bs
       in bs' <$ write_ mat (i :. j) word
  where
    Sz2 n m = sizeOfMArray mat
    isSpace = (== 32)
    isDigit w8 = w8 >= 48 && w8 <= 57
    parseWord bs =
      case BS.uncons bs of
        Just (w8, bs')
          | isDigit w8 -> parseWordLoop (fromIntegral (w8 - 48)) bs'
          | otherwise -> error $ "Unexpected byte: "    show w8
        Nothing -> error "Unexpected end of input"
    parseWordLoop !acc bs =
      case BS.uncons bs of
        Nothing -> (acc, bs)
        Just (w8, bs')
          | isSpace w8 -> (acc, bs')
          | isDigit w8 -> parseWordLoop (acc * 10   fromIntegral (w8 - 48)) bs'
          | otherwise -> error $ "Unexpected byte: "    show w8

Solve

This is the step where we implement the actual solution. Instead of going into trying to fix the solution provided in this SO question I went on and translated the C solution that was linked in the question instead. Reason I went that route is twofold:

C soluition is highly imperative and I wanted to demonstrate that imperative array manipulations are not that foreign to Haskell, so I tried to create a translation that was as close as possible.
I knew that solution works

Note, that it should be possible to rewrite the solution below with array package, because in the end all that is needed are the read, write and allocate operations.

computeSortBy ::
     (Load r Ix1 e, Manifest r' e)
  => (e -> e -> Ordering)
  -> Vector r e
  -> Vector r' e
computeSortBy f vec = 
  withLoadMArrayST_ vec $ quicksortByM_ (\x y -> pure $ f x y) trivialScheduler_

solve :: Matrix P Val -> Maybe (Int, [Color])
solve a = runST $ do
  let sz@(Sz2 n m) = size a
      ord :: Vector P Int
      ord = computeSortBy 
              (\x y -> compare (a ! (y :. 0)) (a ! (x :. 0))) (0 ..: n)
  mxl <- newMArray @P sz minBound
  loopM_ (n - 1) (>= 0) (subtract 1) $ \ i ->
    loopM_ 0 (< m) (  1) $ \j -> do
      writeM mxl (i :. j) (a ! ((ord ! i) :. j))
      when (i < n - 1) $
        writeM mxl (i :. j) 
          =<< max <$> readM mxl (i :. j) <*> readM mxl (i   1 :. j)
      when (j > 0) $
        writeM mxl (i :. j) 
          =<< max <$> readM mxl (i :. j) <*> readM mxl (i :. j - 1)
  mnr <- newMArray @P sz maxBound
  loopM_ (n - 1) (>= 0) (subtract 1) $ \ i ->
    loopM_ (m - 1) (>= 0) (subtract 1) $ \ j -> do
      writeM mnr (i :. j) (a ! ((ord ! i) :. j))
      when (i < n - 1) $
        writeM mnr (i :. j) 
          =<< min <$> readM mnr (i :. j) <*> readM mnr (i   1 :. j)
      when (j < m - 1) $
        writeM mnr (i :. j) 
          =<< min <$> readM mnr (i :. j) <*> readM mnr (i :. j   1)
  mnl <- newMArray @P (Sz m) maxBound
  mxr <- newMArray @P (Sz m) minBound
  let goI i
        | i < n - 1 = do
          loopM_ 0 (< m) (  1) $ \j -> do
            val <- min (a ! ((ord ! i) :. j)) <$> readM mnl j
            writeM mnl j val
            when (j > 0) $
              writeM mnl j . min val =<< readM mnl (j - 1)
          loopM_ (m - 1) (>= 0) (subtract 1) $ \j -> do
            val <- max (a ! ((ord ! i) :. j)) <$> readM mxr j
            writeM mxr j val
            when (j < m - 1) $
              writeM mxr j . max val =<< readM mxr (j   1)
          let goJ j
                | j < m - 1 = do
                    mnlVal <- readM mnl j
                    mxlVal <- readM mxl (i   1 :. j)
                    mxrVal <- readM mxr (j   1)
                    mnrVal <- readM mnr ((i   1) :. (j   1))
                    if mnlVal > mxlVal && mxrVal < mnrVal
                      then pure $ Just (i, j)
                      else goJ (j   1)
                | otherwise = pure Nothing
          goJ 0 >>= \case
            Nothing -> goI (i   1)
            Just pair -> pure $ Just pair
        | otherwise = pure Nothing
  mAns <- goI 0
  Control.Monad.forM mAns $ \ (ansFirst, ansSecond) -> do
    resVec <- createArrayS_ @BL (Sz n) $ \res ->
        iforM_ ord $ \i ordIx -> do
          writeM res ordIx $! if i <= ansFirst then R else B
    pure (ansSecond   1, A.toList resVec)