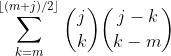The Problem
I need to generate all possible partitions of an integer m into the sum of j elements a_k, where each a_k can be -1, 0, or 1. This is a deterministic algorithm and as such it should be able to implement it at compile time. I would like to return a std::array with all possible combinations as constexpr.
My Algorithm
Plain and simple, there are 3^j combinations in total. So we loop over all of them and check if the sum is m. The total number of valid combinations will be
\sum_{k=m}^{\lfloor (m j)/2\rfloor}\binom{j}{k}\binom{j-k}{k-m}
Thus we can calculate the size of the array (which is j times the number above) and simply queue in all the number combinations we obtain by brute force.
My Code
I obtain the error
error: the value of 'sum' is not usable in a constant expression 88 | if constexpr( sum == m )
I fail to see however, how sum is not known at compile time.
How can I fix this?
#include <array>
#include <iostream>
#include <utility>
/** constexpr for loop **/
template <auto Start, auto End, auto Inc, class F>
constexpr void constexpr_for(F&& f)
{
if constexpr (Start < End)
{
f(std::integral_constant<decltype(Start), Start>());
constexpr_for<Start Inc, End, Inc>(f);
}
}
/** constexpr binomials **/
template<std::size_t n, std::size_t k>
struct Binomial
{
constexpr static std::size_t value = (Binomial<n-1,k-1>::value Binomial<n-1,k>::value);
};
template<>
struct Binomial<0,0>
{
constexpr static std::size_t value = 1;
};
template<std::size_t n>
struct Binomial<n,0>
{
constexpr static std::size_t value = 1;
};
template<std::size_t n>
struct Binomial<n,n>
{
constexpr static std::size_t value = 1;
};
template<std::size_t n, std::size_t k>
constexpr std::size_t binomial()
{
return Binomial<n,k>::value;
}
/** formula from the picture **/
template<std::size_t j, std::size_t m>
constexpr std::size_t n()
{
std::size_t result = 0;
constexpr_for<m, (j m)/2 1, 1>([&result](auto k){
result = binomial<j, k>() * binomial<j-k, k-m>();
});
return result;
}
/** constexpr power function **/
template<std::size_t i, std::size_t j>
struct pow_t
{
constexpr static std::size_t value = i * pow_t<i, j-1>::value;
};
template<std::size_t i>
struct pow_t<i, 0>
{
constexpr static std::size_t value = 1;
};
template<std::size_t i, std::size_t j>
constexpr std::size_t pow()
{
return pow_t<i, j>::value;
}
/** actual function in question **/
template<std::size_t j, std::size_t m>
constexpr std::array<int, j*n<j,m>()> integer_compositions()
{
std::array<int, j*n<j,m>()> result;
std::size_t i = 0;
constexpr_for<0, pow<3, j>(), 1>([&](auto k)
{
std::array<std::size_t, j> partition;
std::size_t sum = 0;
constexpr_for<0, j, 1>([&](auto l)
{
partition[l] = -((k/static_cast<std::size_t>(pow<3,l>()))%3-1);
sum = partition[l];
});
if constexpr( sum == m ) // line 88
{
constexpr_for<0, j, 1>([&](auto l)
{
result[j*i l] = partition[l];
});
i;
}
});
return result;
}
int main()
{
constexpr auto list = integer_compositions<3, 1>();
return EXIT_SUCCESS;
}
CodePudding user response:
You're confusing the purpose of constexpr function. A constexpr function can be executed both at runtime and as part of constant expression, that depends on how you use the function (and probably if the compiler wants to optimize things at compile time).
You don't need all these templated functions, since the whole purpose of constexpr functions is to avoid them for clarity, e.g., your binomial function can simply be:
constexpr std::size_t binomial(std::size_t n, std::size_t k) {
if (k == 0 || n == k) {
return 1;
}
else {
return binomial(n - 1, k - 1) binomial(n - 1, k);
}
}
And you can then do:
// binomial(3, 2) is evaluated at compile-time
std::array<int, binomial(3, 2)> x;
static_assert(x.size() == 3);
This can be done for all of your functions, except the last one (integer_compositions) because the return type depends on the parameter, so you need a template here.
There are other issues in your code, for instance, you need to initialize your std::array in constexpr function, so std::array<..., ...> result{}(note the {} here).
Below is a working version of your code that does not use all of these templates (this requires C 20, but only because operator== for std::array is only constexpr since C 20):
#include <array>
#include <iostream>
/** constexpr binomials **/
constexpr std::size_t binomial(std::size_t n, std::size_t k) {
if (k == 0 || n == k) {
return 1;
}
else {
return binomial(n - 1, k - 1) binomial(n - 1, k);
}
}
/** formula from the picture **/
constexpr std::size_t n(std::size_t j, std::size_t m)
{
std::size_t result = 0;
for (std::size_t k = m; k <= (j m) / 2; k) {
result = binomial(j, k) * binomial(j - k, k - m);
}
return result;
}
/** constexpr power function **/
constexpr std::size_t pow(std::size_t a, std::size_t n) {
std::size_t r = 1;
while (n--) {
r *= a;
}
return r;
}
/** actual function in question **/
template<std::size_t j, std::size_t m>
constexpr std::array<int, j*n(j, m)> integer_compositions()
{
std::array<int, j*n(j, m)> result{};
std::size_t i = 0;
for (std::size_t k = 0; k < ::pow(3, j); k) {
std::array<std::size_t, j> partition{};
std::size_t sum = 0;
for (std::size_t l = 0; l < j; l) {
partition[l] = -((k/static_cast<std::size_t>(::pow(3, l)))%3-1);
sum = partition[l];
}
if (sum == m) // line 88
{
for (std::size_t l = 0; l < j; l) {
result[j*i l] = partition[l];
}
i;
}
}
return result;
}
int main()
{
static_assert(integer_compositions<3, 1>() == std::array<int, 18>{});
}
Note: The static assertion obviously fails because I have no clue what the 18 values are.