The function below is supposed to determine whether two objects of the movingBall struct are "touching" with each other

 bool areBallstouching(movingBall one, movingBall two)
{
    int xMin, xMax, yMin, yMax;
    int TxMin, TxMax, TyMin, TyMax;
    xMin = one.xPosition - one.radius;
    xMax = one.xPosition   one.radius;
    yMin = one.yPosition - one.radius;
    yMax = one.yPosition   one.radius;
    //===================================
    TxMin = two.xPosition - two.radius;
    TxMax = two.xPosition   two.radius;
    TyMin = two.yPosition - two.radius;
    TyMax = two.yPosition   two.radius;
    //=======================================

    vector <int> xrange, yrange, Txrange, Tyrange;
    bool xtouch = false; bool ytouch = false;
    for (int i = xMin; i < xMax; i  )
    {
        xrange.push_back(i);
    }
    for (int i = yMin; i < yMax; i  )
    {
        yrange.push_back(i);
    }
    for (int i = TxMin; i < TxMax; i  )
    {
        Txrange.push_back(i);
    }
    for (int i = TyMin; i < TyMax; i  )
    {
        Tyrange.push_back(i);
    }
    for (int i = 0; i < xrange.size(); i  )
        for (int j = 0; j < Txrange.size(); j  )
            if (xrange[i] == Txrange[j])
                xtouch = true;

    for (int i = 0; i < yrange.size()-1; i  )
        for (int j = 0; j < Tyrange.size()-1; j  )
            if (yrange[i] == Tyrange[j])
                ytouch = true;
    if (xtouch == true && ytouch == true)
    {
        return true;
    }
    else
    {
        return false;
    }
}

I reasoned that the balls can only be touching each other if they share any two coordinates. If they share only an x-coordinate, they will be aligned vertically but the bottom point of the topmost ball will not contact the top point of the bottom-most ball. If they share only a y-coordinate, they will be aligned horizontally but the right-most point of the left-most ball will not touch the left-most point of the right-most ball.

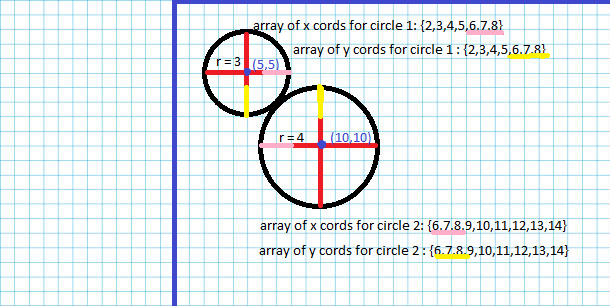
The attached picture demonstrates this reasoning. When I implemented the code, I did not achieve the results I wanted. The program was not able to properly detect the intersections between the two circles.

CodePudding user response：

Mathematically, the point where two circles touch will separate their center positions by a distance equal to the sum of the two radii. It follows:

• if distance between centers is less than the sum of radii, circles intersect;
• if distance between centers is greater than the sum of radii, circles do not intersect (or touch).

So, all you need is a simple distance calculation with basic Pythagoras.

float dx = two.xPosition - one.xPosition;
float dy = two.yPosition - one.yPosition;
float distsq = dx * dx   dy * dy;   // square distance between centers
float r = one.radius   two.radius;  // sum of radii
float rsq = r * r;

bool intersect_or_touch = (distsq <= rsq);

Note that above we can operate in the domain of square distance and square radii to avoid needing to use a sqrt calculation.