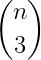I'm working on some heavy algorithm, and now I'm trying to make it multithreaded. It has a loop with 2 nested loops:

for (int i = 0; i < n;   i) {
    for (int j = i   1; j < n;   j) {
        for (int k = j   1; k < n;   k) {
            function(i, j, k);
        }
    }
}

I know, that the number of function calls will be equal to

But I have one last problem: I don't know how to calculate i, j and k based on b (0 <= b < binom(n, 3))

for (int b = start; b < end;   b) {
    // how to calculate i, j, k?
}

How can I calculate these values?

EDIT: My main idea is to call function like this from different threads:

void calculate(int start, int end) {
    for (int b = start; b < end;   b) {
        int i = ...;
        int j = ...;
        int k = ...;
        function(i, j, k);
    }
}

int total = binom(n, 3);

// thread A:
calculate(0, total / 2);

// thread B:
calculate(total / 2, total);

CodePudding user response：

In this post, I shared a class named multi_index which basically does what you want, i.e.

for(auto m : multi_index(3,3,4))
{
    // now m[i] holds index of i-th loop
    // m[0] goes from 0 to 2
    // m[1] goes from 0 to 2
    // m[2] goes from 0 to 3
    std::cout<<m[0]<<" "<<m[1]<<" "<<m[2]<<std::endl;
}

However, this code is for "normal" loops only, where each dimension runs from 0 to some upper value.

In this post, I'll try to apply this to the antisymmetric case where m[i]<m[j] for i<j. The basic idea of the linked code remains the same, namely to create a class that holds the loop boundaries and provides an iterator which can be used with a range-based for loop. The only difference is that I use a std::vector instead of a std::array as the index array type:

#include <iostream>
#include <numeric>
#include <vector>

struct antisym_index_t
{
    int upper_index;
    int dim;
    antisym_index_t(int upper_index, int dim) : upper_index(upper_index), dim(dim) {}

    struct iterator
    {
        struct sentinel_t {};

        int upper_index;
        int dim;
        std::vector<int> index_array = {};
        bool _end = false;

        iterator(int upper_index, int dim) : upper_index(upper_index), dim(dim), index_array(dim)
        {
            std::iota(std::begin(index_array), std::end(index_array),0);
        }

        auto& operator  ()
        {
            for (int i = dim-1;i >= 0;--i)
            {
                if (index_array[i] < upper_index - 1 - (dim-1-i))
                {
                      index_array[i];
                    for (int j = i 1;j < dim;  j)
                    {
                        index_array[j] = index_array[j-1] 1;
                    }                    
                    return *this;
                }
            }
            _end = true;
            return *this;
        }
        auto& operator*()
        {
            return index_array;
        }
        bool operator!=(sentinel_t) const
        {
            return !_end;
        }
    };

    auto begin() const
    {
        return iterator{ upper_index, dim };
    }
    auto end() const
    {
        return typename iterator::sentinel_t{};
    }
};

auto antisym_index(int upper_index, int dim)
{
    return antisym_index_t(upper_index, dim);
}

Note, however, that this code is untested so far (written on top of my head). You can use it as

for(auto m : antisym_index(5,3))
{
    // now m[i] holds index of i-th loop
    std::cout<<m[0]<<" "<<m[1]<<" "<<m[2]<<std::endl;
}

EDIT: by, now, I've tested and corrected the code, see here. Memo to myself: don't publish untested code.

EDIT2: by the way, this answers your question inside the question. It's not clear to me, how this should help with multitasking.

CodePudding user response：

I don't have a full answer, but a solution for 2 loops. My sleep-deprived mind cannot generalize this to 3 loops but maybe someone else can.

In 2D the problem becomes figuring out the row and column index of a triangular matrix from a flattened index. This makes it easy to see that the end that "tapers off" is contained in the larger one. In ASCII art something like this:

      n
 ___________
|_          |
| |_        |
|   |_      |
|   | |_    |
|   |   |_  |
|___|_____|_|
  i   ^
      |
     binom(n-i, 2)

So, let's define

• n loop end index (number of matrix rows/columns)
• i outer loop counter range [0, n). As drawn: column index
• j inner loop counter range [0, i). As drawn: row index from bottom up
• a flattened loop counter range [0, binom(n, 2))

Then i can be computed from binom(n, 2) - binom(n-i, 2) = a. One round-trip through Wolfram Alpha gives us:

• i = trunc(-0.5 * sqrt((1 - 2 n)**2 - 8 a) n - 0.5).

The truncation (=cast to int) "rounds down" to the last full column. So the row index j can be computed from as

• j = a - (binom(n, 2) - binom(n-i, 2))
• j = a - i*(-i 2 n - 1) / 2