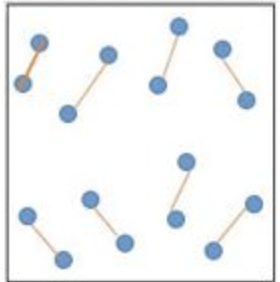
Given a list of 2*N points in a plane, I am trying to find a method which will divide them into N pairs such that each pair has a similar edge length to all other pairs.

Essentially I am trying to form pairs of points which are roughly equidistant.

CodePudding user response：

I can propose only naive solution. Not pretty sure about its time complexity, but it's polynomial, and for sure not worse than O(n^5) :)

Let's make some definitions:

• p1 and p2 — our points. Structure of point contains its index, so for each pair of point we can know is it the same point or else. p1.i — index of p1.
• D(p1, p2) — distance between p1 and p2. In implementation it would be convenient to store squares of distances, in order to use int type. So D(p1, p2) = (p1.x - p2.x)^2 (p1.y - p2.y)^2.
• SameDistanceMap is a map from distance to array of point's pairs, such as:

For each (p1, p2) in SameDistanceMap[dst], D(p1, p2) = dst.

You can do it this way:

1. Let's construct SameDistanceMap. It can be easily done with double nested loop.
2. Now we know, that if answer exists, then it's a subarray of one of SameDistanceMap value-arrays.
3. Let's iterate SameDistanceMap value-arrays, and see if any one of them is a real answer. We can consider only arrays of length not less then n.
4. Let's consider each of these arrays. The rest of the task could be reformulated to