depth-first search algorithm to traverse a graph using open and closed list-CodePudding

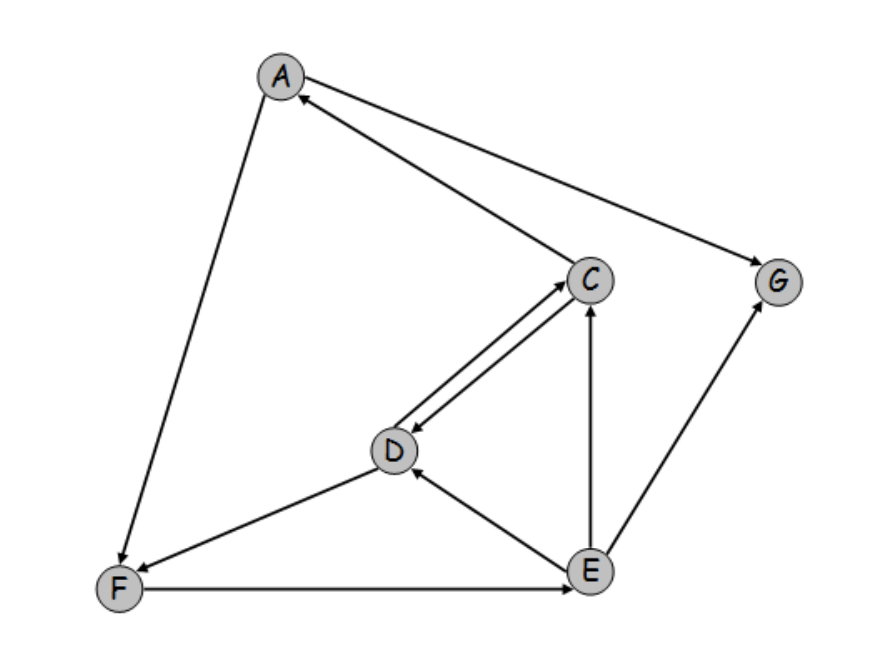
I need to use the depth first search algorithm on the graph linked within the picture, and I need to use open and closed lists to show the result/outcome.

I currently have the following:

N	Open	Closed
1	`[A]`	`[]`
2	`[A,F]`	`[]`
3	`[A,F,E]`	`[]`
4	`[A,F,E,G]`	`[]`
5	`[A,F,E,G,D]`	`[]`
6	`[A,E,G,D]`	`[F]`
7	`[A,E,G,D,C]`	`[F]`
8	`[A,G,D,C]`	`[F,E]`
9	`[A,G,D,C]`	`[F,E]`
10	`[A,G,C]`	`[F,E,D]`
11	`[A,G]`	`[F,E,D,C]`
12	`[G]`	`[F,E,D,C,A]`
13	`[]`	`[F,E,D,C,A,G]`

Can anyone assist me in regards to whether this is correct, or if it is incorrect can you please help me understand why with the correct answer and an explanation?

Thanks in advance

CodePudding user response：

Expanding the states by alphabetical order from Node A the below is the Open/Closed list maintained for Depth First Search traveral for the above graph. Answer:

CodePudding user response：

What exactly do open and closed mean in this context of this problem?

In Prolog a closed list is a list terminated by the atom [], representing the empty list.

In bracketed list notation that would be a list like this:

[a,b,c]

In formal ./2 notation, that list is represented by this Prolog structure:

.( a , .( b , .( c , [] ) ) )

Whilst the same list as an open list is this:

[ a , b , c | Some_Unbound_Variable ]

or in ./2 notation:

.( a , .( b , .( c , Some_Unbound_Variable ) ) )

I do not believe that that is what you're looking for. Please explain.

Your graph looks to be a directed, cyclic graph, which is to say that edges may be traversed only in one direction (One can travel from A to G, but not from G to A), and that it contains cycles, meaning that starting from one node within the graph and traversing the graph, you will eventually get back to your origin (a cycle). And that leads to endless loops, unless you track the places you've been.

You may represent your graph thus:

edge( a , f ).
edge( a , g ).
edge( c , a ).
edge( c , d ).
edge( d , c ).
edge( d , f ).
edge( e , c ).
edge( e , d ).
edge( e , g ).
edge( f , e ).

And traversing a graph is pretty trivial:

traverse( Origin, Destination, Path ) :-
  edge(Origin,_),
  traverse( Origin, Destination, [Origin] , Path )
  .

traverse( A, B , Vs , [B|Vs] ) :- % we can get from A to B
  edge(A,B)                       % - if A and B are directly connected.
  .                               % otherwise...
traverse( A, B , Vs , P      ) :- % we can get from A to B
  edge(A,X) ,                     % - if we can get from A to some X
  X \== B   ,                     % - such that X is not B
  \ memberchk(X,Vs) ,             % - and that we have not yet visited X
  traverse(X,B,[X|Vs],P)          % - and see if we can get from X to B
  .                               %

Upon success, Path should be unified with the path taken through the graph in reverse order, so using your graph as an example, Path = [G,E,F,A] says that you traveled G <- E <- F <- A.

CodePudding user response：

To get the answer given by @J013R, you can use the following program:

dfs_traversal(Root) :-
   format('Open    Closed        Visited\n'),
   dfs_traversal([Root], [], -).

dfs_traversal(Open, Closed, Visited) :-
   format('~|~w~t~7  ~|~w~t~13  ~w\n', [Open, Closed, Visited]),
   (   Open = [Node|Rest]
   ->  findall(Successor, successor(Node, Open, Closed, Successor), Successors),
       append(Successors, Rest, NewOpen),
       dfs_traversal(NewOpen, [Node|Closed], Node)
   ;   true ).

successor(Node, Open, Closed, Successor) :-
   arc(Node, Successor),
   not(member(Successor, Open)),
   not(member(Successor, Closed)).

arc(a, f).
arc(a, g).
arc(c, a).
arc(c, d).
arc(d, c).
arc(d, f).
arc(e, c).
arc(e, d).
arc(e, g).
arc(f, e).

Example:

?- dfs_traversal(a)
Open    Closed        Visited
[a]     []            -
[f,g]   [a]           a
[e,g]   [f,a]         f
[c,d,g] [e,f,a]       e
[d,g]   [c,e,f,a]     c
[g]     [d,c,e,f,a]   d
[]      [g,d,c,e,f,a] g
true.