I understand how to do this using right triangles: the length of my desired vector will be the magnitude of vector a divided by the cosine of the angle between vector a and the given unit vector. Once I find this value, I can simply scale the unit vector by this length.

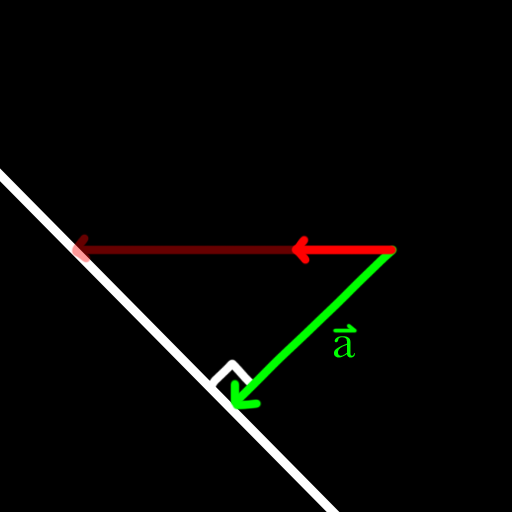
Assuming that the dot product of the normalized vector a and the given unit vector is greater than 0, how can I find this length using only vector math? Below is a picture to help illustrate what I'm trying to do. I want the red vector, which will be a unit vector, to be scaled until it meets the white line that is perpendicular with vector a.

CodePudding user response：

We start with the green vector a and the red unit vector r.

Normalize a to get a unit vector we'll call k:

k = a/|a|

Now project r onto k to get the component of r in the direction of a, call it x (which is equal to the cosine of the angle between r and a).

x = r · k = (1/|a|)(r · a)

Now we use similar triangles:

|R|/|a| = |r|/x = 1/x

|R| = |a|/x

R = |R|r = (|a|/x)r = (|a|²/(r · a))r