Updating a binary tree using a pointer-CodePudding

I'm trying to update a self-balancing binary tree. Normally, you can update it by 1) searching a node, 2) deleting it, 3) and inserting the tree with a new node. But, I want to see if this is possible simply by retaining a pointer to a node from the first step and updating it so that I can bypass the deletion and insertion and improve the time complexity, especially when it comes to a large number of nodes.

The tree itself is standard binary search tree.

public class TreeNode<T: Comparable>: Equatable {
    public typealias Node = TreeNode<T>
    
    var key: T?
    var leftChild: Node?
    var rightChild: Node?
    fileprivate weak var parent: Node?
    
    var isNullLeaf: Bool {
        return key == nil && isLeaf
    }
    
    var isLeaf: Bool {
        return rightChild == nil && leftChild == nil
    }
    
    public init(key: T?, leftChild: Node?, rightChild: Node?, parent: Node?) {
        self.key = key
        self.leftChild = leftChild
        self.rightChild = rightChild
        self.parent = parent
        
        self.leftChild?.parent = self
        self.rightChild?.parent = self
    }
    
    /// Null leaf
    public convenience init() {
        self.init(key: nil, leftChild: nil, rightChild: nil, parent: nil)
    }
    
    static public func == <T>(lhs: TreeNode<T>, rhs: TreeNode<T>) -> Bool {
        return lhs.key == rhs.key
    }
}

public final class Tree<T: Comparable> {
    public typealias Node = TreeNode<T>
    
    fileprivate(set) var root: Node
    fileprivate let nullLeaf = Node()
    
    public init() {
        root = nullLeaf
    }
    
    func search(key: T, f: (inout Node) -> Void) {
        search(key: key, node: &root, f:  f)
    }

    fileprivate func search(key: T, node: inout Node, f: (inout Node) -> Void) {
        if !node.isNullLeaf {
            if let nodeKey = node.key {
                /// When a node is found, pass by reference as an argument to a closure so that it retains the connection to the node when it's being update.
                if key == nodeKey {
                    f(&node)
                } else if key < nodeKey {
                    guard node.leftChild != nil else {
                        return
                    }
                    search(key: key, node: &node.leftChild!, f: f)
                } else {
                    guard node.rightChild != nil else {
                        return
                    }
                    search(key: key, node: &node.rightChild!, f: f)
                }
            }
        }
    }

    public func insert(key: T) {
       /// insertion logic
    }
    
    /// Other operations
}

My idea was to search the tree through recursion and when a node is found, pass it as an argument to a closure function, which will ultimately be called to update the node. Also, the found node would be pass by reference.

class Test<T: Comparable> {
    private(set) var tree = Tree<T>()
    
    func insert(key: T) {
        tree.insert(key: key)
    }
    
    func update(for node: T, with newNode: T) {
        tree.search(key: node) { foundNode in
            foundNode.key = newNode
        }
    }
}

let test = Test<MyNode>()
let node = MyNode()
let anotherNode = MyNode()
test.insert(key: node)
test.update(for: node, with: anotherNode)

The problem is the update doesn't happen. If I search for newly updated node in the tree, it doesn't exist.

Update

Above code is a modified version of a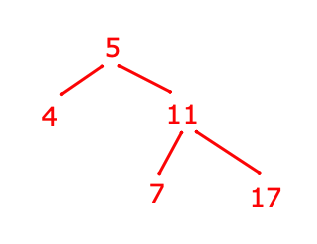

And printing the BFS traversal shows us this:

Test 2
Inserting 5
Inserting 11
Inserting 4
Inserting 7
Inserting 17
Current tree before update

** PRINTING BST IN LEVEL ORDER (BFS) ** 
5
4
11
7
17

print("Updating 7 with 16")
test.update(for: 7, with: 16)
print("Current tree after update")
test.display()

Now Let's try to change the value of 7 with 16 which is done with the pointer

print("Updating 7 with 16")
test.update(for: 7, with: 16)
print("Current tree after update")
test.display()

The output is as expected with the value of 7 and swapped with 16

Updating 7 with 16
Current tree after update

** PRINTING BST IN LEVEL ORDER (BFS) ** 
5
4
11
16
17

Ofcourse, after this swap, the tree is no longer a Binary Search Tree but I think you can see the pointer working well with the above tweaks.