Here is a code to exponentiate a number to a given power:

#include <stdio.h>

int foo(int m, int k) {
    if (k == 0) {
        return 1;
    } else if (k % 2 != 0) {
        return m * foo(m, k - 1);
    } else {
        int p = foo(m, k / 2);
        return p * p;
    }
}

int main() {
    int m, k;
    while (scanf("%d %d", &m, &k) == 2) {
        printf("%d\n", foo(m, k));
    }
    return 0;
}

How do I calculate the time complexity of the function foo?

I have been able to deduce that if k is a power of 2, the time complexity is O(log k).

But I am finding it difficult to calculate for other values of k. Any help would be much appreciated.

CodePudding user response：

How do I calculate the time complexity of the function foo()?

I have been able to deduce that if k is a power of 2, the time complexity is O(logk).

First, I assume that the time needed for each function call is constant (this would for example not be the case if the time needed for a multiplication depends on the numbers being multiplied - which is the case on some computers).

We also assume that k>=1 (otherwise, the function will run endlessly unless there is an overflow).

Let's think the value k as a binary number:

If the rightmost bit is 0 (k%2!=0 is false), the number is shifted right by one bit (foo(m,k/2)) and the function is called recursively.

If the rightmost bit is 1 (k%2!=0 is true), the bit is changed to a 0 (foo(m,k-1)) and the function is called recursively. (We don't look at the case k=1, yet.)

This means that the function is called once for each bit and it is called once for each 1 bit. Or, in other words: It is called once for each 0 bit in the number and twice for each 1 bit.

If N is the number of function calls, n1 is the number of 1 bits and n0 is the number of 0 bits, we get the following formula:

N = n0   2*n1   C

The constant C (C=(-1), if I didn't make a mistake) represents the case k=1 that we ignored up to now.

This means:

N = (n0   n1)   n1   C

And - because n0 n1 = floor(log2(k)) 1:

floor(log2(k))   C <= N <= 2*floor(log2(k))   C

As you can see, the time complexity is always O(log(k))

CodePudding user response：

O(log(k))

Some modification added to output a statistics for spread sheet plot.

#include <stdio.h>
#include <math.h>

#ifndef TEST_NUM
#define TEST_NUM (100)
#endif

static size_t iter_count;

int foo(int m, int k) {
  iter_count  ;

  if (k == 0) {
    return 1;
  } else if(k == 1) {
    return m;      
  } else if (k % 2 != 0) {
    return m * foo(m, k - 1);
  } else {
    int p = foo(m, k / 2);
    return p * p;
  }
}

int main() {
  for (int i = 1; i < TEST_NUM;   i) {
    iter_count = 0;
    int dummy_result = foo(1, i);
    printf("%d, %zu, %f\n", i, iter_count, log2(i));
  }
  return 0;
}
```C

Build it.
```Bash
gcc t1.c -DTEST_NUM=10000
./a > output.csv

Now open the output file with a spread sheet program and plot the last two output columns.

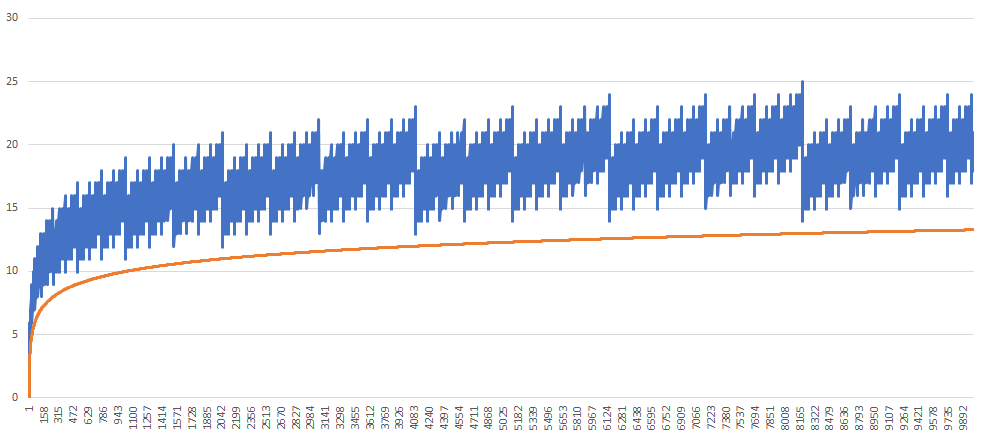
CodePudding user response：

For k positive, the function foo calls itself recursively p times if k is the p-th power of 2. If k is not a power of 2, the number of recursive calls is strictly inferior to 2 * p where p is the exponent of the largest power of 2 inferior to k.

Here is a demonstration:

let's expand the recursive call in the case k % 2 != 0:

int foo(int m, int k) {
    if (k == 1) {
        return m;
    } else
    if (k % 2 != 0) {  /* 2 recursive calls */
        // return m * foo(m, k - 1);
        int p = foo(m, k / 2);
        return m * p * p;
    } else {           /* 1 recursive call */
        int p = foo(m, k / 2);
        return p * p;
    }
}

The total number of calls is floor(log2(k)) bitcount(k), and bitcount(k) is by construction <= ceil(log2(k)).

There are no loops in the code and the time of each individual call is bounded by a constant, hence the overall time complexity of O(log k).