How to plot PSD in dBFS?-CodePudding

The following code I have written measures PSD of the signal y by taking FFT first.

Fsig=26e3;           % signal frequency
Fs = 1e6;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
N = 2^15;             % Length of signal
t = (0:N-1)*T;        % Time vector

y=sin(2*pi*Fsig*t)   harmonics; // a sine function with harmonics

% find FFT PSD
xdft = fft(y);
xdft = xdft(1:N/2 1);
psdx = (1/(Fs*N)) * abs(xdft).^2;
psdx(2:end-1) = 2*psdx(2:end-1);
freq = 0:Fs/N:Fs/2;
psdx_log=10*log10(psdx);

% plot PSD
figure(1)
plot(frq,psdx_log,'r')
ylim([-150 0])
grid on
title('Periodogram Using FFT')
xlabel('Frequency (Hz)')
ylabel('Power/Frequency (dB/Hz)')

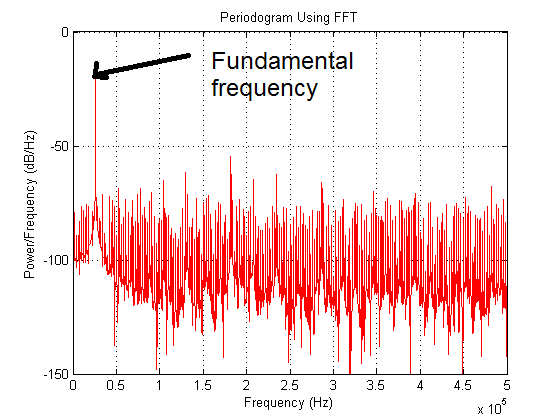
Here's the output:

As you see the spectrum contains various harmonics in addition to the fundamental frequency. However, this plot is not ideally what I want. I want to plot PSD in dBFS where the fundamental tone, the sine wave, is at 0 dBFS so that all harmonics are measured relative to this 0 dBFS reference. What to do?

CodePudding user response：

You can normalize the PSD, thus the maximum of the PSD will be 0dB (if some harmonic is higher than the signal you should adapt the value to normalize):

Fsig=26e3;           % signal frequency
Fs = 1e6;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
N = 2^15;             % Length of signal
t = (0:N-1)*T;        % Time vector

y=sin(2*pi*Fsig*t)   harmonics; // a sine function with harmonics

% find FFT PSD
xdft = fft(y);
xdft = xdft(1:N/2 1);
psdx = (1/(Fs*N)) * abs(xdft).^2;
psdx(2:end-1) = 2*psdx(2:end-1);
freq = 0:Fs/N:Fs/2;
psdx_log=10*log10(psdx./max(psdx));

% plot PSD
figure(1)
plot(frq,psdx_log,'r')
ylim([-150 0])
grid on
title('Periodogram Using FFT')
xlabel('Frequency (Hz)')
ylabel('Power/Frequency (dB/Hz)')