I have an ODE which I would like to solve using compiled C code called from R's deSolve package. The ODE in question is I an exponential decay model (y'=-d* exp(g* time)*y): But running the compiled code from within R gives different results to R's native deSolve. It's as is there they are flipped 180º. What's going on?

C code implementation

/* file testODE.c */
#include <R.h>
static double parms[4];
#define C parms[0] /* left here on purpose */
#define d parms[1]
#define g parms[2]

/* initializer  */
void initmod(void (* odeparms)(int *, double *))
{
  int N=3;
  odeparms(&N, parms);
}

/* Derivatives and 1 output variable */
void derivs (int *neq, double t, double *y, double *ydot,
             double *yout, int *ip)
{
  // if (ip[0] <1) error("nout should be at least 1");
  ydot[0] = -d*exp(-g*t)*y[0];
}
/* END file testODEod.c */

R implementation - Native deSolve

  testODE <- function(time_space, initial_contamination, parameters){
  with(
    as.list(c(initial_contamination, parameters)),{
      dContamination <- -d*exp(-g*time_space)*Contamination
      return(list(dContamination))
    }
  )
}

parameters <- c(C = -8/3, d = -10, g =  28)
Y=c(y=1200)
times <- seq(0, 6, by = 0.01)
initial_contamination=c(Contamination=1200) 
out <- ode(initial_contamination, times, testODE, parameters, method = "radau",atol = 1e-4, rtol = 1e-4)

plot(out)

R implementation - Run compiled code from deSolve

library(deSolve)
library(scatterplot3d)
dyn.load("Code/testODE.so")

Y <-c(y1=initial_contamination) ;
out <- ode(Y, times, func = "derivs", parms = parameters,
           dllname = "testODE", initfunc = "initmod")


plot(out)

CodePudding user response：

Compiled code does not give different results to deSolve models implemented in R, except potential rounding errors within the limits of atoland rtol.

The reasons of the differences in the original post where two errors in the code. One can correct it as follows:

1. Declare static double as parms[3]; instead of parms[4]
2. Time t in derivs is a pointer, i.e. *t

so that the code reads as:

/* file testODE.c */
#include <R.h>
#include <math.h>

static double parms[3];
#define C parms[0] /* left here on purpose */
#define d parms[1]
#define g parms[2]

/* initializer  */
void initmod(void (* odeparms)(int *, double *)) {
  int N=3;
  odeparms(&N, parms);
}

/* Derivatives and 1 output variable */
void derivs (int *neq, double *t, double *y, double *ydot,
             double *yout, int *ip) {
  ydot[0] = -d * exp(-g * *t) * y[0];
}

Here the comparison between the two simulations, somewhat adapted and generalized:

library(deSolve)

testODE <- function(t, y, parameters){
  with(
    as.list(c(y, parameters)),{
      dContamination <- -d * exp(-g * t) * contamination
      return(list(dContamination))
    }
  )
}

system("R CMD SHLIB testODE.c")
dyn.load("testODE.dll")

parameters <- c(c = -8/3, d = -10, g =  28)
Y          <- c(contamination = 1200)
times      <- seq(0, 6, by = 0.01)

out1 <- ode(Y, times, testODE,
            parms = parameters, method = "radau", atol = 1e-4, rtol = 1e-4)
out2 <- ode(Y, times, func = "derivs", dllname = "testODE", initfunc = "initmod",
            parms = parameters, method = "radau", atol = 1e-4, rtol = 1e-4)

plot(out1, out2)          # no visible difference
summary(out1 - out2)      # differences should be (close to) zero

dyn.unload("testODE.dll") # always unload before editing .c file !!

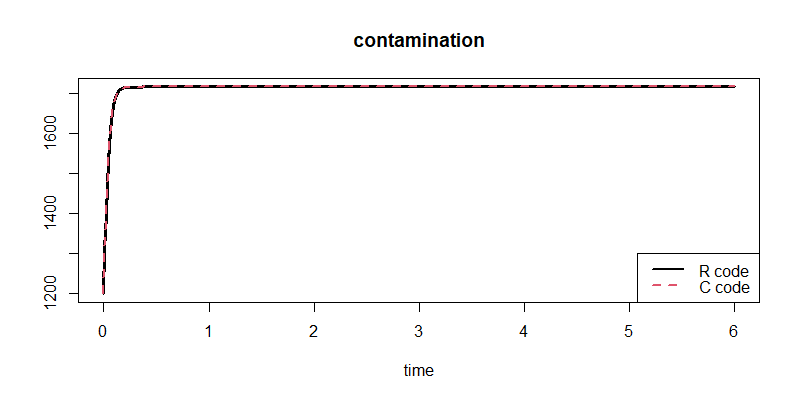
Note: set.dll or .so according to your OS, or detect it with .Platform$dynlib.ext.