I am in need of help proving that an algorithm has greedy choice property and optimal substructure.

Context of the problem:

Consider a problem where a company owns n gas stations that are connected by a highway. Each gas station has a limited supply g_i of gas-cans. Since the company don't know which gas station is most visited they want all of them to have the same amount of gas.

So they hire a fueling-truck to haul gas between the stations in their truck. However, truck also consumes 1 gas-can per kilometer driven.

Your task will be to help the chain calculate the largest amount of gas-cans g_bar they can have at all Stations.

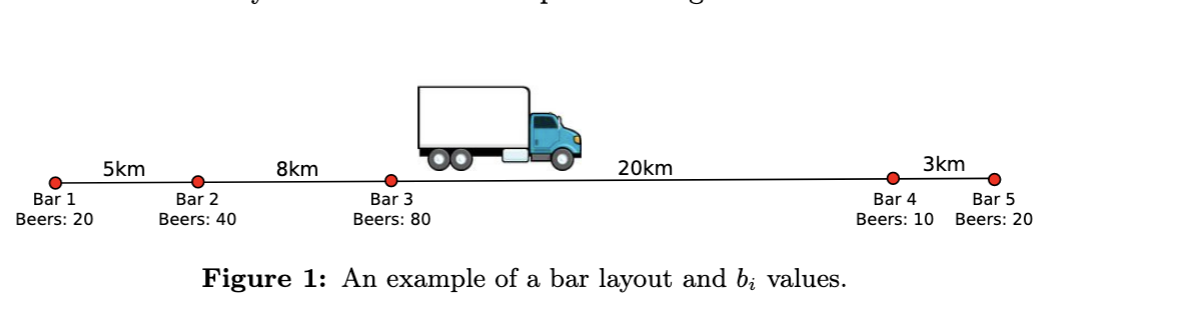
Consider the example: Here we have g = (20, 40, 80, 10, 20) and p = (0, 5, 13, 33, 36) (in kilometers). In order to send one gas-can from station 3 to station 4 we need to put 41 gas-cans in the truck, as the fueling-truck will consume 40 before reaching their destination (to send two gas-cans we need to put 42 in the truck). The optimal g_bar for the example is 21 and can be achieved as follows:

1. Station 2 sends 11 gas-cans towards Station 1. One gas-can arrives while ten are consumed on the way.

2. Station 3 sends 59 gas-cans towards Station 4. 19 arrive while 40 are consumed on the way.

3. Station 4 now has 29 gas-cans and send eight towards Station 5. Two of these arrive and six are consumed on the way.

4. The final distribution of gas-cans is: (21, 29, 21, 21, 22).

Given an integer g_bar. Determine whether it is possible to get at least g_bar gas-cans in every Gas Station.

in order for the greedy choice property and optimal substructure to make sense for a decision problem, you can define an optimal solution to be a solution with at least g_bar gas-cans in every gas station if such a solution exists; otherwise, any solution is an optimal solution.

Input: The position p_i and gas-can supply g_i of each bar. Here g_i is the supply for the bar at position p_i. You may assume that the positions are in sorted order – i.e. p_1 < p_2 < . . . < p_n.

Output: The largest amount g_bar, such that each gas-station can have a gas-can supply of at least g_bar after the truck have transferred gas-cans between the stations.

Visualization but replace beer with gas-cans and gas-stations with bars:

Algorithm:

def Gas_algorithm(Gas,pos,g_bar):
    n = len(Gas)
    Gas = Gas.copy()
    for i in range(n - 1): 
        if Gas[i] >= g_bar:   
            iCanSpare = Gas[i] - 2 * (pos[i   1] - pos[i]) - g_bar 
            if iCanSpare > 0: 
                Gas[i   1]  = iCanSpare  
        else:             
            Gas[i   1] -= g_bar - Gas[i]   2 * (pos[i   1] - pos[i]) 
            Gas[i] = g_bar  

    if Gas[n - 1] < g_bar:    
        return 0           
        
    return 1               

How can i prove Greedy Choice and Optimal Substructure for this?

CodePudding user response：

Let's define an optimal solution: Each station has at least X gas cans in each station (X = g_bar).

Proving greedy property

Let us assume our solution is sub-optimal. There must exist a station i such that gas[i] < X. Based on our algorithm, we borrow X - gas[i] from station i 1 (which is a valid move, since we had already found a solution). Now station i has gas = X. This contradicts the original assumption that there must exist a station i such that gas[i] < X, which means our solution isn't suboptimal. Hence, we prove the optimality.

Proving optimal substructure

Assume we have a subset of the stations of size N', and our solution is suboptimal. Again, if the solution is suboptimal, there must exist a station i such that gas[i] < X. You can use the greedy proof again to prove that our solution isn't suboptimal. Since we have optimal solution for each arbitrary subset, we prove that we have optimal substructure.