I have multiple dataframes (different years) that looks like the following dataframe. Each dataframe contains the share of wealth each id holds (across equally distributed 1000 units of x-axis bins. So for instance, if there are 4,000,000 individuals, each bin will represent the sum of 4,000 individuals in descending order). What I want is to plot this in one chart. I am lacking creatibity as to what is the best to way to show these very skewed wealth distribution across different years...
When i look at my dataframe from year 2021, the top 0.1 holds 92% of all wealth. So when I plot it using a bar chart, it looks like just one straight vertical line, and if i use a line chart, it is a L-shaped graph. I was thinking maybe i should have different x-axis bin width, as in, insteady of using 1000 equal sized bins on the a-axis, maybe the top 0.1%, top 0.1-0.5%, top 0.5-1%, 1-5%, 5-10%, 10-20%,... etc.
If anyone has a good idea, i'd really really appreciate it!
x wealth_share_2016
1 0.33430437283205316
2 0.08857907028903435
3 0.05827083476711605
4 0.03862747269456592
5 0.034995688078949164
6 0.025653645763917113
7 0.021026627708501285
8 0.018026751734878957
9 0.01642864468243111
10 0.015728925648574896
11 0.013588290634843092
12 0.01227954727973525
13 0.011382643296594532
14 0.010141965617682762
15 0.008819245941582449
..
1000 0.000000000011221421
x wealth_share_2017
0.0 0.901371131515615
1.0 0.029149650261610725
2.0 0.01448219525035078
3.0 0.00924941242097224
4.0 0.006528547368042855
5.0 0.004915282901262396
6.0 0.0038227195841958007
7.0 0.003202422960559232
8.0 0.0027194902152005056
9.0 0.002256081738439025
10.0 0.001913906326353021
11.0 0.001655920262049755
12.0 0.001497315358785623
13.0 0.0013007783674694787
14.0 0.0011483994993211357
15.0 0.0010006446573525651
16.0 0.0009187314949837794
17.0 0.0008060306765341464
18.0 0.0007121683663280601
19.0 0.0006479765506981805
20.0 0.0006209618807503557
21.0 0.0005522371927723867
22.0 0.0004900821167110386
23.0 0.0004397140637940455
24.0 0.00039311806560654995
25.0 0.0003568253540177216
26.0 0.00033181209459040074
27.0 0.0003194446403240109
28.0 0.0003184084588259308
29.0 0.0003182506069381648
30.0 0.0003148797013444408
31.0 0.0002961487376129427
32.0 0.00027052175379974156
33.0 0.00024743766685454786
34.0 0.0002256857592625916
35.0 0.00020579998427225097
36.0 0.000189038268813506
37.0 0.00017386965729266948
38.0 0.0001613485014690905
39.0 0.0001574132034911388
40.0 0.0001490677750078641
41.0 0.00013790177558791725
42.0 0.0001282878615396144
43.0 0.00012095612436994448
44.0 0.00011214167633915717
45.0 0.00010421673782294511
46.0 9.715626623684205e-05
47.0 9.282271063116496e-05
48.0 8.696571645233427e-05
49.0 8.108410275243205e-05
50.0 7.672762907247785e-05
51.0 7.164556991989368e-05
52.0 6.712091046340094e-05
53.0 6.402983760430654e-05
54.0 6.340827259447476e-05
55.0 6.212579456204865e-05
56.0 6.0479432395632356e-05
57.0 5.871255187231619e-05
58.0 5.6732218205513816e-05
59.0 5.469844909188562e-05
60.0 5.272638831110061e-05
61.0 5.082941624023762e-05
62.0 4.9172657560503e-05
63.0 4.7723292856953955e-05
64.0 4.640794539328976e-05
65.0 4.4830504104868853e-05
66.0 4.33432435988776e-05
67.0 4.17840819038174e-05
68.0 4.0359335324500254e-05
69.0 3.890539627505912e-05
70.0 3.773843593447448e-05
71.0 3.650676651396156e-05
72.0 3.528219096983737e-05
73.0 3.440527767945646e-05
74.0 3.350747980104347e-05
75.0 3.26561659597071e-05
76.0 3.19802966664897e-05
77.0 3.1835209823474306e-05
78.0 3.183429293715699e-05
79.0 3.183429293715699e-05
80.0 3.179465449554639e-05
81.0 3.1754468203569435e-05
82.0 3.1704945367497785e-05
83.0 3.1660515386167146e-05
84.0 3.161204511239972e-05
85.0 3.160031088406889e-05
86.0 3.160031088406889e-05
87.0 3.159054611415194e-05
88.0 3.1527283185355765e-05
89.0 3.1443493604304305e-05
90.0 3.1323353389521874e-05
91.0 3.117894171029721e-05
92.0 3.0954278315859144e-05
93.0 3.057844960395481e-05
94.0 3.014447137763062e-05
95.0 2.9597164606371073e-05
96.0 2.887863910263771e-05
97.0 2.8423195872524498e-05
98.0 2.7793813070448293e-05
99.0 2.7040901735687525e-05
100.0 2.619028564470109e-05
101.0 2.5450004510283205e-05
102.0 2.4855217140189223e-05
103.0 2.403822662596923e-05
104.0 2.3244772756237742e-05
... ...
1000.0 0.000000023425324
CodePudding user response:
Binning these data across irregular percentage ranges is a common way to present such distributions. You can categorize and aggregate data using pd.cut() with subsequent group_by():
import pandas as pd
import matplotlib.pyplot as plt
#sample data generation
import numpy as np
rng = np.random.default_rng(123)
n = 1000
df = pd.DataFrame({"x": range(n), "wealth_share_2017": np.sort(rng.pareto(a=100, size=n))[::-1]})
df.loc[0, "wealth_share_2017"] = 50
df["wealth_share_2017"] /= df["wealth_share_2017"].sum()
n = len(df)
#define bins in percent
#the last valueis slightly above 100% to ensure that the final bin is included
bins = [0, 0.1, 0.5, 1.0, 10.0, 50.0, 100.01]
#create figure labels for intervals from bins
labels = [f"[{start:.1f}, {stop:.1f})" for start, stop in zip(bins[:-1], bins[1:])]
#categorize data
df["cats"] = pd.cut(df["x"], bins=[n*i/100 for i in bins], include_lowest=True, right=False, labels=labels)
#and aggregate
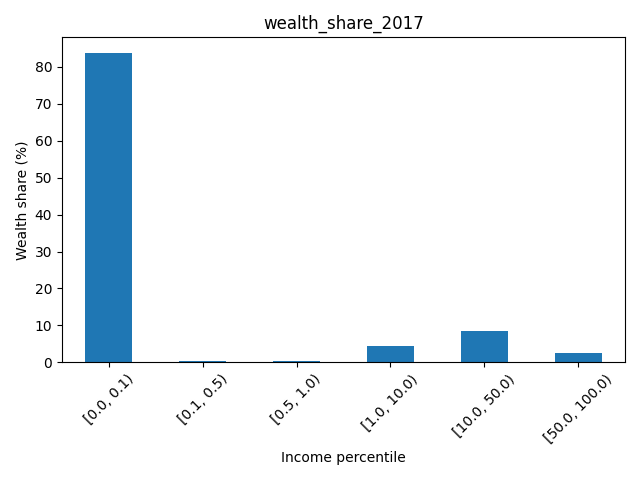
df_plot = df.groupby(by="cats")["wealth_share_2017"].sum().mul(100)
df_plot.plot.bar(rot=45, xlabel="Income percentile", ylabel="Wealth share (%)", title=df_plot.name)
plt.tight_layout()
plt.show()