Cumulative integration of sin(x)/x-CodePudding

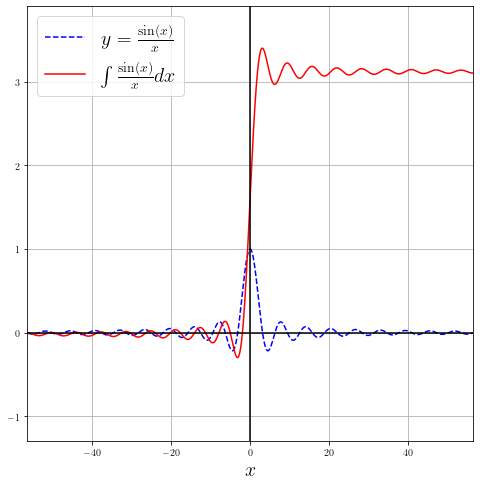
I'm trying to plot the integral of sin(x)/x by means of obtaining a cumulative sum of the area beneath sin(x)/x.

def y(x):
a = np.sin(x) / x
a[np.isnan(a)] = 1 # (Lim y(x)--> 0) = 1
return a

I tried using a for loop for a left Riemann sum:

a = -56.5
b = 56.5
n = 1000
x = np.linspace(a,b,n)
I = np.zeros(n)

for i in range(n):
    I[i] = (y(x[:i 2])).sum()*(b-a)/n

Using np.cumsum():

I = np.cumsum(y(x))*(b-a)/n

And using scipy.integrate with trapezoid method:

from scipy import integrate
I = integrate.cumulative_trapezoid(y(x), x, initial=0)

All the methods mentioned give the following:

But according to Wolfram Alpha the expected behavior should look like:

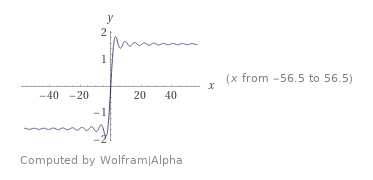
As you can see, the integral takes values between [-2, 2] (roughly speaking), but by doing cumulative sums it takes values out of that range, and it worsens as one make use of bigger intervals. Any ideas on why this is the case? I'm very likely having a severe case of tunnel-vision here, so I would appreciate any comments.

CodePudding user response：

Wolfram is calculating/graphing, Si(x), defined as the integral of sin(x) / x between 0 and x.

If you change a to 0 and b to any positive number or b to 0 and a to any negative number, you will see that the integral lies within that rough -2 to 2 band you mentioned.

That Wolfram graph is not meant to coincide with your cumulative sum graph. The -2 to 2 band does not represent the range of possible values one can get from integrating sin(x) / x over some interval.

FYI, the limit of Si(x) as x gets arbitrarily large is pi / 2. Similarly, the limit of Si(x) as x approaches negative infinity is -pi / 2.