How to add neighboring elements of 2D array in Python without having to use nested loops?-CodePudding

I want to add neighboring elements "3x3" of an array and create new array. When using nested loops, it takes time since this piece of code will be called thousands of times.

import tensorflow as tf
import numpy as np

rows=6
cols=8

array1 = np.random.randint(10, size=(rows, cols))
print(array1)

array2=np.zeros((rows-2,cols-2))

for i in range(rows-2):
    for j in range(cols-2):
        array2[i,j]=np.sum(array1[i:i 3,j:j 3])# print()
        
print("output\n",array2)


##My output
    [[9 4 9 6 1 4 9 0]
     [2 3 4 2 0 0 9 0]
     [2 8 9 7 6 9 4 8]
     [6 3 6 7 7 0 7 5]
     [2 1 4 1 7 6 9 9]
     [1 1 2 6 3 8 1 4]]
    output
     [[50. 52. 44. 35. 42. 43.]
     [43. 49. 48. 38. 42. 42.]
     [41. 46. 54. 50. 55. 57.]
     [26. 31. 43. 45. 48. 49.]]

With vectorization, this can be solved. However, I tried different techniques but never had luck with any such as reshaping then adding arrays, using only one loop with size rows or cols. note: in my project, the size of rows and cols can be very big. it is similar to 2D convolution with kernal of ones. the question is, is there anyway to implement this without using loops? or at least reduce it to have smaller time complexity "to take only rows or cols as size of loop".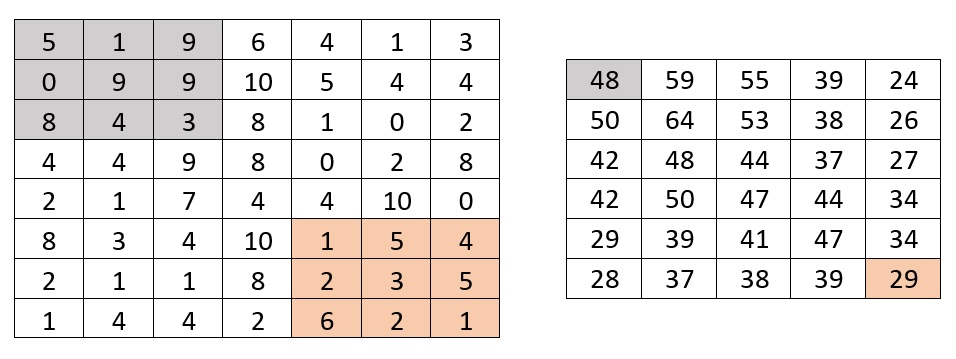

CodePudding user response：

Here you should use partial sum. and you could find any point in 1 operation.

If you use it for small numbers. There is no a lot of performance difference. But If you check it with big numbers. You will see performance difference.

rows = count of row

cols = count of cols

innerrow = your aim row. *//in your example(3)*

innercol = your aim col. *//in your example(3)*

With your code:

O(rows x cols x innerrow x innercol)

O(2000 x 2000 x 200 x 2000)

But you could calculate it with:

O(rows x cols)

example: O(2000 x 2000)

import numpy as np

rows = 1000
cols = 2000

array1 = np.random.randint(10, size=(rows, cols))
array0 = array1
print(array1)

array2 = np.zeros((rows-100, cols-100))

for i in range(0, rows):
    for j in range(1, cols):
        array1[i][j]  = array1[i][j-1]

for i in range(0, cols):
    for j in range(1, rows):
        array1[j][i]  = array1[j-1][i]

for i in range(rows-100):
    for j in range(cols-100):
        sm = array1[i 100][j 100]
        if i-1 >= 0:
            sm -= array1[i-1][j 100]
        if j-1 >= 0:
            sm -= array1[i 100][j-1]
        if i-1 >= 0 and j-1 >= 0:
            sm  = array0[i-1][j-1]
        array2[i, j] = sm

print("output\n", array2)

And here is output

[[1 9 1 9 2 0 3 8]
 [7 1 8 7 1 2 8 4]
 [7 1 5 4 8 3 9 0]
 [4 4 8 9 3 1 7 6]
 [2 5 9 9 3 6 7 2]
 [9 0 9 5 0 3 2 8]]
output
 [[40. 45. 45. 36. 36. 37.]
 [45. 47. 53. 38. 42. 40.]
 [45. 54. 58. 46. 47. 41.]
 [50. 58. 55. 39. 32. 42.]]

CodePudding user response：

I got the solution that i find better for this cases. Use the function convolve2d from scipy.signal module I used the function np.ones and np.array to declare your input as a numpy array and used the convolve2d to apply your kernel to each an every part of your image. This is called Convolutional Filters and Kernels and it is used a lot in image processing with python.

In [50]: import numpy as np

In [55]: np.ones((3,3))
Out[55]: 
array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])

In [59]: input
Out[59]: 
array([[9, 4, 9, 6, 1, 4, 9, 0],
       [2, 3, 4, 2, 0, 0, 9, 0],
       [2, 8, 9, 7, 6, 9, 4, 8],
       [6, 3, 6, 7, 7, 0, 7, 5],
       [2, 1, 4, 1, 7, 6, 9, 9],
       [1, 1, 2, 6, 3, 8, 1, 4]])

In [60]: kernel
Out[60]: 
array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])

In [61]: from scipy.signal import convolve2d

In [62]: convolve2d(input, kernel)
Out[62]: 
array([[ 9., 13., 22., 19., 16., 11., 14., 13.,  9.,  0.],
       [11., 18., 31., 28., 22., 13., 23., 22., 18.,  0.],
       [13., 28., 50., 52., 44., 35., 42., 43., 30.,  8.],
       [10., 24., 43., 49., 48., 38., 42., 42., 33., 13.],
       [10., 22., 41., 46., 54., 50., 55., 57., 42., 22.],
       [ 9., 14., 26., 31., 43., 45., 48., 49., 35., 18.],
       [ 3.,  5., 11., 15., 23., 31., 34., 37., 23., 13.],
       [ 1.,  2.,  4.,  9., 11., 17., 12., 13.,  5.,  4.]])

In [63]: convolve2d(input, kernel, 'valid')
Out[63]: 
array([[50., 52., 44., 35., 42., 43.],
       [43., 49., 48., 38., 42., 42.],
       [41., 46., 54., 50., 55., 57.],
       [26., 31., 43., 45., 48., 49.]])

Also, as a matter of fact the speed of this is quite fast. As you can see, even in a 1000x1000 matrix it's fast enough.

In [68]: %timeit convolve2d(input, kernel, 'valid')
5.24 µs ± 21.2 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

In [69]: input = np.random.randint(10, size=(1000, 1000))

In [70]: %timeit convolve2d(input, kernel, 'valid')
41.6 ms ± 555 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

I hope this answer helps you.