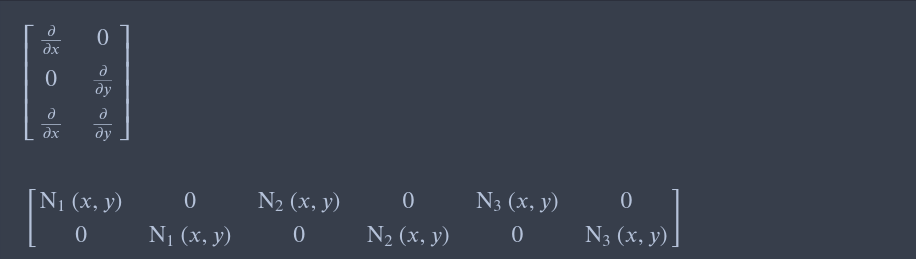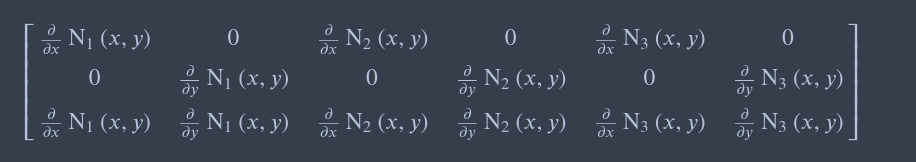Delta operator in sympy-CodePudding

Is it possible to make a delta operator like this in sympy? Im not really sure how to code it. Should be really eazy if there exists a method.

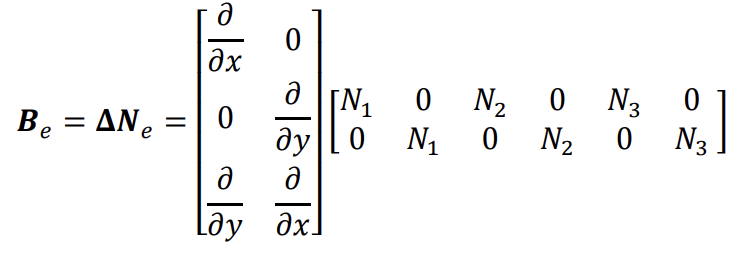
CodePudding user response：

I don't know if SymPy exposes something that could be useful to you. If not, we can create something raw.

Note: the following approach requires a bit of knowledge in Object Oriented Programming and the way SymPy treats things. This is a 5 minutes attempt, and it is not meant to be used in production (as a matter of fact, no test has been done over this code). There are many things that may not work as expected. But, for your case, it might work :)

One possible way is to define a "gradient" class, like this:

class Grad(Expr):
    def __mul__(self, other):
        return other.diff(*self.args)
    def _latex(self, printer):
        # create a latex representation to be visualize in Jupyter Notebook
        return r"\frac{\partial}{%s}" % " ".join([r"\partial %s" % latex(t) for t in self.args])

We can create a gradient of something with respect to x by writing gx = Grad(x). Once gx is multiplied with some other thing, it returns the partial derivative of that thing with respect to x.

Then you would define your symbols/functions and matrices like this:

from sympy import *
init_printing()
var("x, y")
N1, N2, N3 = [s(x, y) for s in symbols("N1:4", cls=Function)]
A = Matrix(3, 2, [Grad(x), 0, 0, Grad(y), Grad(x), Grad(y)])
B = Matrix(2, 6, [N1, 0, N2, 0, N3, 0, 0, N1, 0, N2, 0, N3])
display(A, B)

Finally, you multiply the matrices together to obtain the symbolic results:

A * B

Eventually, you might want to create a function:

def delta_operator(x, y, N1, N2, N3):
    A = Matrix(3, 2, [Grad(x), 0, 0, Grad(y), Grad(x), Grad(y)])
    B = Matrix(2, 6, [N1, 0, N2, 0, N3, 0, 0, N1, 0, N2, 0, N3])
    return A * B

So, whenever you have to apply that operator, you just execute delta_operator(x, y, N1, N2, N3) to obtain a result similar to above.