Have I applied the Fourier Transformation correctly to this Dataframe? [EXAFS X-Ray Absorption Dataf-CodePudding

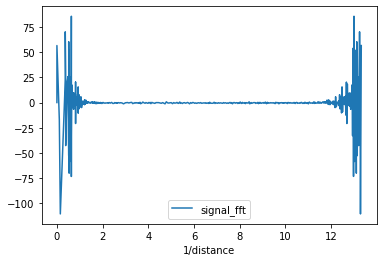
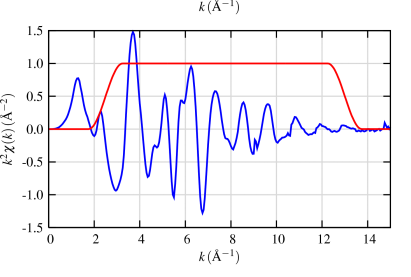
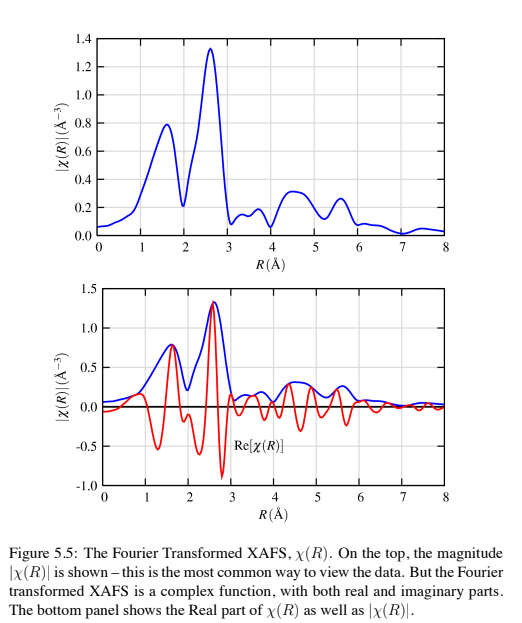
I have a dataset with a signal and a 1/distance (Angstrom^-1) column.

This is the dataset (fourier.csv):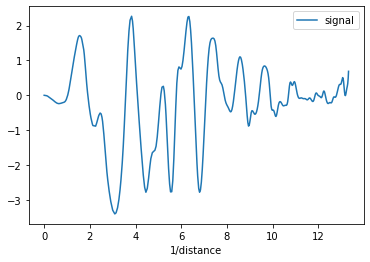

To generate the Fast Fourier Transformation data, I used the numpy library for its fft function and I applied it like this:

df['signal_fft'] = fft(df['signal'])

df.plot(x ='1/distance', y ='signal_fft', kind = 'line')

Now the plot looks like this, with the FFT data plotted instead of the initial "signal" data:

What I hoped to generate is something like this (This signal is extremely similar to mine, yet yields a vastly different FFT picture):

Theory Signal before windowing:

$!\Theory Signal$

Theory FFT:

As you can see, my initial plot looks somewhat similar to graphic (a), but my FFT plot doesn't look anywhere near as clear as graphic (b). I'm still using the 1/distance data for both horizontal axes, but I don't see anything wrong with it, only that it should be interpreted as distance (Angstrom) instead of 1/distance (1/Angstrom) in the FFT plot.

How should I apply FFT in order to get a result that resembles the theoretical FFT curve?

Here's another slide that shows a similar initial signal to mine and a yet again vastly different FFT:

CodePudding user response：

I have a dataset with a signal and a 1/distance (Angstrom^-1) column.

This is the dataset (fourier.csv):

(Y is the difference, X is the index in the dataframe.)

This is supposed to be a constant line.

In order to fix this, one solution is to resample the signal through linear interpolation so that the timestep is constant.

from scipy import interpolate

rs_df = df.drop_duplicates().copy()  # Needed because 0 is present twice in dataset
x = rs_df['1/distance']
y = rs_df['signal']
flinear = interpolate.interp1d(x, y, kind='linear')
xnew = np.linspace(np.min(x), np.max(x), rs_df.index.size)
ylinear = flinear(xnew)

rs_df['signal'] = ylinear
rs_df['1/distance'] = xnew
df.plot(x ='1/distance', y ='signal', kind = 'line')
rs_df.plot(x ='1/distance', y ='signal', kind = 'line')

The new line looks visually identical, but has a constant timestep.

I still don't get your intended result from the FFT, so this is only a partial solution.