I'm writing signal source for digital signal processing and found strange behaviour. Here is the code:

    float complex *output = malloc(sizeof(float complex) * 48000);
    FILE *f = fopen("test_signal.cf32", "wb");
    int64_t freq = -3355;
    float phase_increment = 2 * (float) M_PI * (float) freq / 48000;
    float phase = 0.0F;
    for (int i = 0; i < 150 * 5; i  ) {
        for (int j = 0; j < 9600; j  ) {
            output[j] = cosf(phase)   sinf(phase) * I;
            phase  = phase_increment;
        }
        fwrite(output, sizeof(float complex), 9600, f);
    }
    fclose(f);

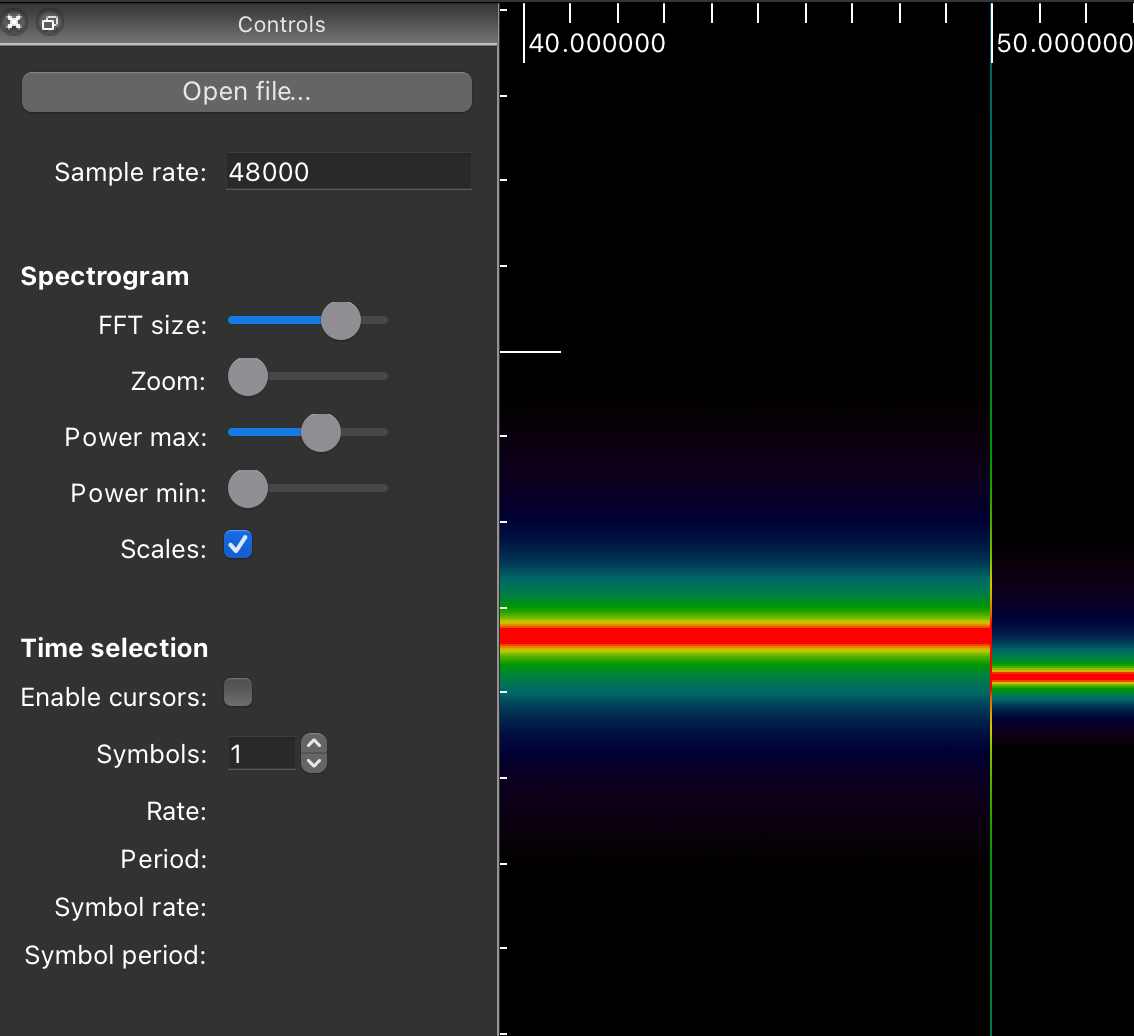
It will create a file with complex signal shifted by -3355hz from the centre. So when I run FFT over this file I expect a signal at -3355hz. With some minor frequency distribution around that number due to quantisation. But in reality I'm getting the following:

There is a quite significant frequency jump (~2000hz) around 50 seconds.

Anyone knows why?

My experiments showed:

• using double for the phase helps
• doing argument reduction from -2pi to 2pi helps
• Apple M1 and raspberry pi have the same jump
• there seems to be no overflow in the phase argument
• Fun reading https://randomascii.wordpress.com/2014/10/09/intel-underestimates-error-bounds-by-1-3-quintillion/ but unlikely causing sudden jump of a frequency

CodePudding user response：

Once phase gets large enough, increments to it are quantized by floating-point rounding, maybe enough that rounding to nearest with tie-break of rounding to even mantissa doesn't balance out, and instead means you consistently advance the phase less. See wikipedia's article on single-precision IEEE float

A base-10 analogy with values limited to 4 significant figures would be 101.2 0.111 only going up to 101.3, not 101.311. (Computers use binary floats, so actually stuff like 101.125 is exactly representable where 101.1 isn't.)

I suspect that's what's happening. You won't overflow to Inf, but given the limited relative precision of a float, adding a small number to a huge number will eventually not move it at all: the closest representable float to phase phase_increment will be the original phase.

A quick way to test this hypothesis would be to use double phase (without making any other changes), and see if that moves the point at which you get frequency steps. (To be vastly greater, probably past the end of what you're generating).

(Oh, just noticed you already did that, and it did help. If you mean it completely removed the problem, then that's probably it.)

You can still keep the single-precision sinf and cosf, although changing them would be the other thing to try: as @Weather Vane points out, some sin implementations lose significant precision in range-reduction. But you'd expect that to be a noisier signal, not a consistent change in frequency (which would take a scale factor for the phase.)

You could also let it run longer with float and see if you get another step down in frequency, or a change all the way to DC (constant phase, frequency = 0).

Or with float, manually unroll so you have two counters offset by phase_increment and you increment each one by 2*phase_increment. So the relative magnitude of phase vs. what's being added doesn't get so extreme. They'll still get to the same absolute magnitude, though, large relative to the original phase_increment, so there will still be some rounding.

I don't know if there are better strategies for generating complex sine waves, I'm just trying to explain the behaviour you're seeing.

For performance of this method, you probably want sincosf to compute both values at the same time, if your compiler doesn't optimize your calls into that. (And hopefully auto-vectorize by calling a SIMD sincosf.)

CodePudding user response：

What you observing is floating point precision issues. Precision of floats degrades with magnitude.

Fortunately, for phases or similar angular values there’s an easy workaround, wrap the value around 2π so the magnitude is never too large.

Add the following code after your phase = phase_increment; and see if that helps.

if( phase < (float)( 2.0 * M_PI ) )
    continue;
phase -= (float)( 2.0 * M_PI );