How to compute Kramers-Moyal coefficients when the time step is not to small in Python?-CodePudding

I am coding a simple one-dimensional Ornstein-Uhlenbeck simulation in python to explain some experimental data from a video source, i.e., tracking a brownian particle in a sequence of frames. The sampling frequency of the camera is fps=30 frames per seconds, which means that my time resolution is dt=0.03 seconds, approximately. On the other hand, the smallest time scale I am able to measure is about tau=0.5 seconds, one order of magnitude larger than dt (a reasonable difference to be able to compute observables such as autocorrelation functions of the process).

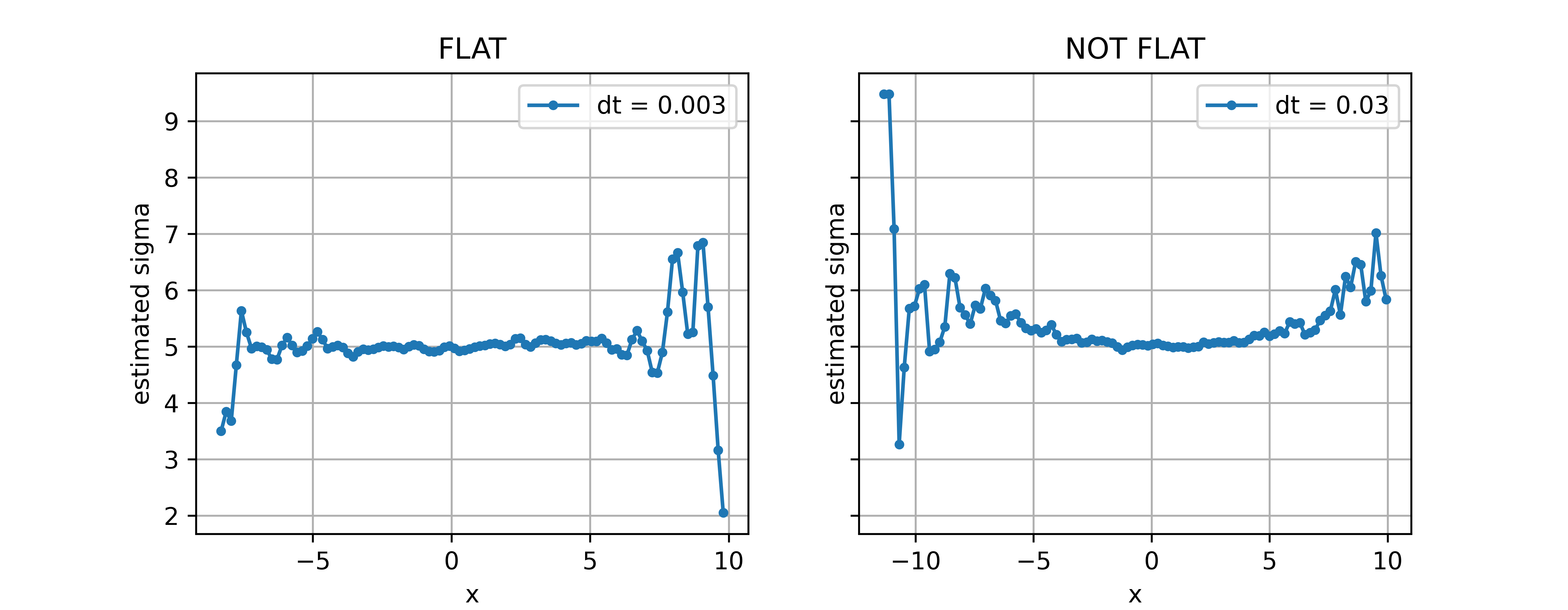
Now, for the simulated data I am computing the first two Kramers-Moyal coefficients using kramersmoyal. The problem arises ONLY with the second coefficient when dt is not at least two order of magnitudes smaller than tau, in which case the estimation for the noise intensity becomes convex instead of a flat function.

So the questions at hand are:

is there a simple way to code some corrections to address this issue?
is there any other package that deals with this problem?
is this an implementation problem or just a consequence that these coefficients are defined in the limit of infinitely small time steps (i.e., dt->0)?

In order to be more concrete, the code bellow shows the simulation for two different time steps, dt, that differs in two and one order of magnitude from tau, respectively. Then the second coefficient is computed for both cases and the noise intensity of the processes are estimated. The noise intensity looks flat for the first case but not for the second.

# === Ornstein-Uhlenbeck simulation ===

import numpy as np
import kramersmoyal as km
import matplotlib.pyplot as plt

np.random.seed(0)

n = 100_000       # total number of time steps
dt = [.003, .03]  # time steps two/one order of magnitud smaller than tau
tau = .5          # relaxation or characteristic time
sigma = 5         # noise intensity

scale_dW = sigma * np.sqrt(dt)    # scale parameter of the Wiener process
scale_x = sigma / np.sqrt(2/tau)  # scale parameter of the process under study

dW = np.random.normal(scale=scale_dW, size=(n, 2))  # Wiener process array
x = np.empty((n, 2))                                # x array
x[0] = np.random.normal(scale=scale_x, size=2)      # initial condition

# Euler-Maruyama method to solve the SDE
for i in range(n - 1):
    x[i   1] = x[i] - 1/tau * x[i] * dt   dW[i]

# === Second Kramers-Moyal coefficient ===

fig, axs = plt.subplots(1, 2, sharey=True, figsize=(9,3.5))
bins = np.array([100])         # number of bins
powers = np.array([[1], [2]])  # first and second power

for i in range(len(dt)):
    # computation of the coefficients using `kramersmoyal`
    kmc, edges = km.km(x[:,i], bins, powers)

    # sigma parameter estimation
    sigma_est = np.sqrt(2 * kmc[1] / dt[i])

    # plotting
    axs[i].plot(edges[0], sigma_est, '.-', label=f'dt = {dt[i]}')
    axs[i].legend()
    axs[i].set_title(['FLAT', 'NOT FLAT'][i])
    axs[i].set_xlabel('x')
    axs[i].set_ylabel('estimated sigma')
plt.show()

CodePudding user response：

tl;dr: Add the correction to the diffusion as

D₂(x) = (M₂(x) - (M₁(x)²)/2)/dt

or using the kmc in your notation

sigma_est = np.sqrt(2 * (kmc[1] - 0.5*kmc[0]**2) / dt[i])

This is actually a known "issue", which arises from the mathematical approximation to expressing the Kramers-Moyal operator when solving the Kramers-Moyal equation (or similarly the Fokker-Planck equation). You can find a first-ish example of this problem in On the definition and handling of different drift and diffusion estimates, New Journal of Physics 10, 083034, 2008.

To get straight to the answer, there is a finite-time correction to the second Kramers-Moyal coefficient given by

D₂(x) = (M₂(x) - (M₁(x)²)/2)/dt

This should immediately correct the convexity (or quadratic effect) you observe. It is truly a finite-time effect.

You can find a full set of corrections for all Kramers-Moyal coefficients in Arbitrary-Order Finite-Time Corrections for the Kramers–Moyal Operator, Entropy, 23(5), 517, 2021.

Disclosure: I am one of the authors of both the kramersmoyal python library and the last mentioned publication.