Say I have an undirected graph where I have already determined the articulations points (i.e. nodes that, when removed, will disconnect the graph). Next, I want to remove/add a node to this graph and determine how the articulation points change. Is there an algorithm that can use the previously calculated articulation points to speed up the calculation or is starting from scratch after every node addition/removal my only choice?

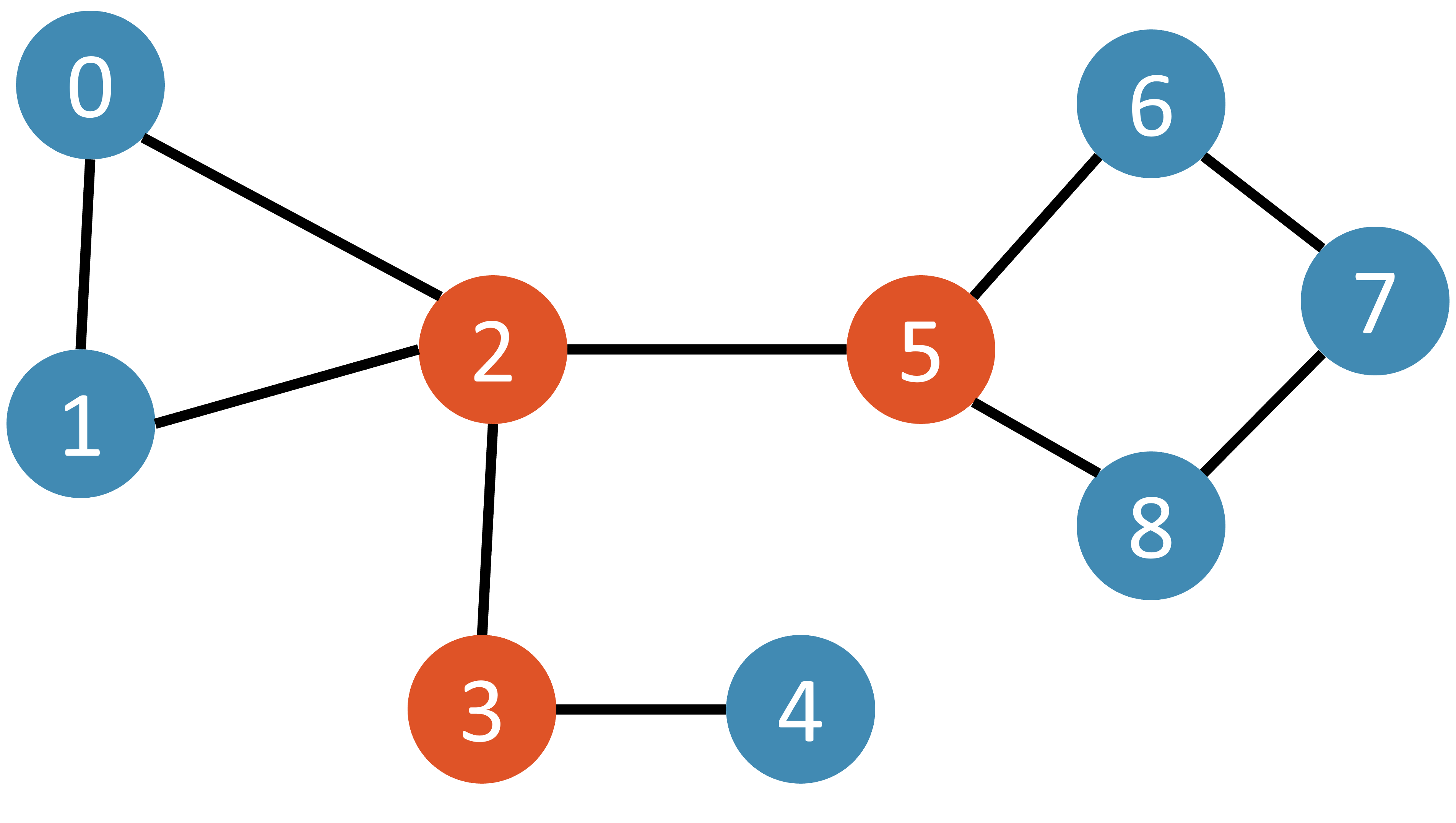
Just for clarity, in the example graph below nodes 2, 3, and 5 are articulation points. If I remove node 4, 3 is no longer an articulation point. If I add node 9 connected to nodes 4 and 8, nodes 3 and 5 are no longer articulation points. I'm not sure how to generalize this process.

CodePudding user response：

Generally speaking, you may have to spend Θ(n) work updating the list of articulation points. To see this, imagine your graph is just a path with n nodes. Initially, all your nodes are articulation points. Adding a new node that closes the path into a cycle will make it so that none of your nodes are articulation points, and then deleting any of those nodes will once again make everything an articulation point.

The above point means that there isn’t going to generally be a fast algorithm for recomputing all the articulation points because there are bad pathological cases. However, if you’re okay with something a bit weaker than this, there are approaches that allow for fast insertions and deletions. Specifically, there are algorithms/data structures that solve the fully dynamic biconnectivity problem. These data structures allow you to add and delete nodes and edges from a graph and, as you do, to query whether a pair of nodes are biconnected (belong to the same biconnected component). This isn’t an exact match for what you’re looking for, but it may be helpful if your goal is to determine which nodes will remain connected after a node deletion. The drawback is that these are fairly tricky data structures / algorithms to implement.