I don't know how can I solve OpenCV Python problem-CodePudding

The original assignment is

Use np.array() to generate the following 8-bit image and obtain the result of applying the following mask: 
However, the edges are padded to zero. (cv2.BORDER_CONSTANT)

[[10, 20, 40, 50]
 [50, 20, 50, 20]
 [10, 10, 30, 60]
 [20, 40, 60, 70]]

(a) 3x3 average filter
(b) 3x3 gaussian filter, sigmaX=0
(c) If the results of (a) and (b) are M(x,y) and G(x,y), 
    respectively, calculate M(0,0) and G(0,0) and show that 
    they are consistent with the results of (a) and (b).

The problem is,

(a) - 3x3 average filter

(b) - 3x3 gaussian filter, sigmaX=0

And the result of (a) is M(x, y) and the result of (b) is G(x, y)

So I should show that M(0, 0) and G(0, 0) are correct.

I wrote code, but I can't solve this problem.

How can I solve this problem ....

The code -

import cv2
import numpy as np

src = np.array([[10, 20, 40, 50],
                 [50, 20, 50, 20],
                 [10, 10, 30, 60],
                 [20, 40, 60, 70]], dtype=np.uint8)

dst1 = cv2.blur(src, ksize=(3, 3), borderType=cv2.BORDER_CONSTANT)
dst2 = cv2.GaussianBlur(src, ksize=(3, 3), sigmaX=0, borderType=cv2.BORDER_CONSTANT)

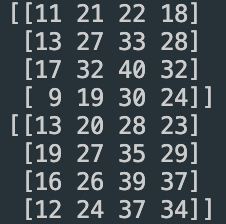
print(dst1)
print(dst1[0][0])
print(dst2)
print(dst2[0][0])
print(dst1[0][0] == dst2[0][0])

The result -

M(0, 0) is 11(dst1[0][0]) and G(0, 0) is 13(dst2[0][0])

I mean, I need to make dst1[0][0] and dst2[0][0] match.

but the result does not match.

Sorry for my bad English skill .....

CodePudding user response：

it's an assignment, so i wont solve it completely for you, but here are some hints:

so, convolution is the sum of a per-element multiplication between your filter kernel and a pixel neighbourhood of the same size.

at 0,0 - given zero padding, the latter looks like this:

0.0  0.0  0.0
0.0 10.0 20.0
0.0 50.0 20.0

and a 3x3 box kernel looks like this:

1.0/9 1.0/9 1.0/9 
1.0/9 1.0/9 1.0/9
1.0/9 1.0/9 1.0/9

so, M(0,0) is:

1.0/9 *  0.0   1.0/9 *  0.0   1.0/9 *  0.0   
1.0/9 *  0.0   1.0/9 * 10.0   1.0/9 * 20.0  
1.0/9 *  0.0   1.0/9 * 50.0   1.0/9 * 20.0  == 11.11111

and you have to show, that M(0,0) == dst1[0,0]

float values used here to avoid rounding issues. please use np.float32, not np.uint8 in your opencv code to achieve the same.

here's the gaussian kernel, hopefully you know, what to do now, good luck ;)