Premise

A simple SDL program of an entity (single dot/pixel) that rotates around (in a circle), then moves in that direction.

Problem

I'm unable to properly calculate the shortest distance from one degree to another; especially when those degrees cross the bounds of the 360/0 mark.

Goal

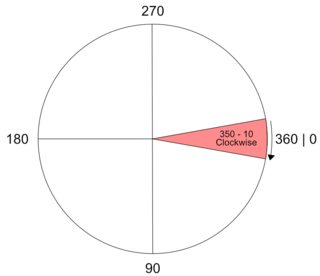
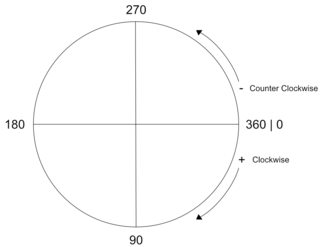
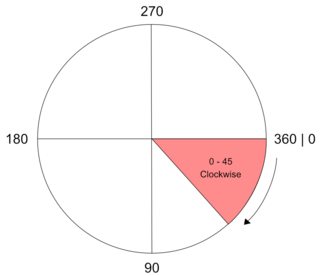
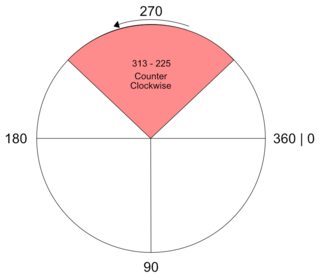
Calculate whether the shortest distance from an 'origin' degree to a 'destination' is Clockwise, or Counter Clockwise, while factoring in the transversal over the 360 degree mark.

Program Display

Attempting to fulfill these concepts

Code

Main

void draw ( )
{
    /* - - - - - - - - - - - - - - - - - Init - - - - - - - - - - - - - - - - - */
    
    SDL_Event sdl_event;

    WALKER walker;
    
    walker = { POINT { WINDOW_WIDTH / 2, WINDOW_HEIGHT / 2 } };    // Entity in center

    /* - - - - - - - - - - - - - - - - - Init - - - - - - - - - - - - - - - - - */
    
    int degree = 0;
    
    walker.rotation.set ( degree, generate_random ( 0, 360 ) );
    
    while ( run_loop )     // Display Animation
    {
        set_render_draw_colors ( );
        
        SDL_RenderDrawPoint ( renderer, walker.origin.x, walker.origin.y );     // Draw: entity dot

        POINT point = walker.rotate ( degree );     // Create: pivot point & rotate per degree

        SDL_RenderDrawLine ( renderer, walker.origin.x, walker.origin.y, point.x, point.y );     // Draw: sightline with acquired orientation

        SDL_RenderPresent ( renderer );

        degree  ;

        degree = ( degree > 359 ) ? 0 : degree;

        if ( degree == walker.rotation.destination )
            walker.rotation.set( walker.rotation.destination, generate_random ( 0, 360 ) );
        
        while ( SDL_PollEvent ( &sdl_event )  )
        {
            if ( sdl_event.type == SDL_QUIT )
                run_loop = false;
            else
                break;
        }
    }
}

Walker

struct WALKER
{
    POINT origin     = { 0, 0 };
    POINT point      = { 0, 0 };

    ROTATION rotation;
    
    int point_length = 35;
    
    time_t time_seed;
    
    // Constructors ......................................................... //
    
    WALKER ( POINT origin, POINT point )
    {
        this->origin = origin;
        this->point  = point;
    }
    
    // Constructors (Generic) ... //
    
    WALKER ( )  { };

    ~WALKER ( ) { };

    // Functions ............................................................ //

    double convertToRadian ( int degree )
    {
        return ( degree * PI / 180 );
    }

    int convertToDegree ( float radian )
    {
        return ( radian * 180 ) / PI;
    }
    
    POINT rotate ( int degree )
    {
        POINT point    = { this->origin.x   this->point_length, this->origin.y };
        
        double radians = convertToRadian ( degree );
        
        double sine    = sin ( radians );
        double cosine  = cos ( radians );

        point.x       -= this->origin.x;     // translate point back to origin
        point.y       -= this->origin.y;

        double x_new  = point.x * cosine - point.y * sine;     // rotate point
        double y_new  = point.x * sine   - point.y * cosine;
        
        point.x       = x_new   this->origin.x;     // translate point back
        point.y       = y_new   this->origin.y;
        
        return point;
    }
};

CodePudding user response：

If it wasn't for the 0/360 cross, it would just be a matter of getting the difference between the two angles, the sign of that difference would tell you if it's clockwise or not.

On, top of that, if you get the difference between two angles for which the shortest path DOES cross the boundary, you'd end up with a difference with an absolute value greater than 180 (since the distance ends up going around the circle the other way.

So all you need to do is get the difference between the two angles, and "fix" it if it's too large.

int angle_diff(int from, int to) {
  // Use a modulo to handle angles that go around the circle multiple times.
  int result = to % 360 - from % 360;

  if(result > 180) {
      result -= 360;
  }

  if(result <= -180) {
      result  = 360;
  }
  return result;
}