I construct a Newton polynomial based on a given simple sine function. Implemented intermediate calculations, but stopped at the final stage - to obtain the formula of the polynomial. Recursion may help here, but it's inaccurate. Here is the formula of the polynomial

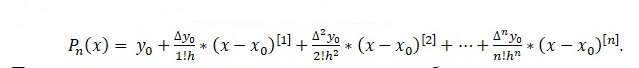
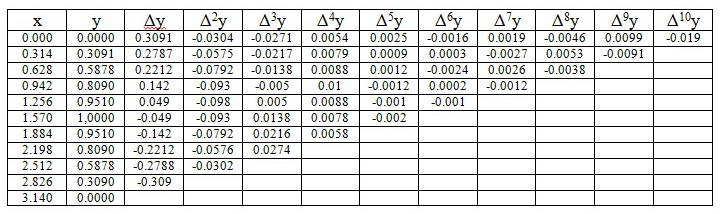
The formula iterates over the values from the table below: we go through the column of x's and the first line of the calculated deltas (we go up to the delta, which degree of the polynomial we get). For example, if the degree is 2, then we will take 2 deltas in the first row and values up to 2.512 in the column of x (9 brackets with x differences will be in the last block of the polynomial)

In the formula, there is a set of constant blocks where values are iterated through, but I have a snag in the element (x —x_0)**[n]. This is the degree of the polynomial n that the user sets. Here [n] means that the expression in the parenthesis is expanded: 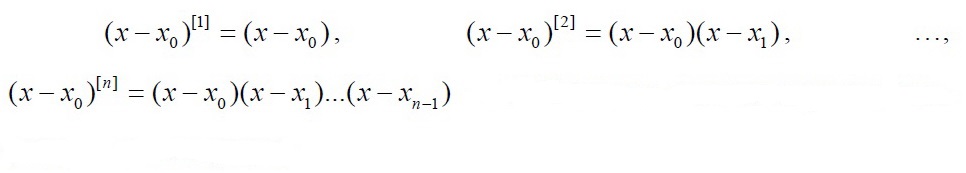I use the sympy library for symbolic calculations: x in the formula of the future polynomial should remain x (as a symbol, not its value). How to implement a part of a block repeating in a polynomial that grows with a new bracket of the degree of the polynomial?

Code:

import numpy as np
from sympy import *
import pandas as pd
from scipy.special import factorial

def func(x):
    return np.sin(x)

def poly(order):
    # building columns X and Y:
    x_i_list = [round( (0.1*np.pi*i), 4 ) for i in range(0, 11)]
    y_i_list = []
    for x in x_i_list:
        y_i = round( (func(x)), 4 ) 
        y_i_list.append(y_i)

    # we get deltas:
    n=order
    if n < len(y_i_list):
        result = [ np.diff(y_i_list, n=d) for d in np.arange(1, len(y_i_list)) ]
        print(result)
    else:
        print(f'Determine the order of the polynomial less than {len(y_i_list)}')
        
    # We determine the index in the x column based on the degree of the polynomial:
    delta_index=len(result[order-1])-1
    x_index = delta_index
    h = (x_i_list[x_index] - x_i_list[0]) / n   # calculate h
    
    
    b=x_i_list[x_index]
    a=x_i_list[0]
    y_0=x_i_list[0]
    string_one = [] # list with deltas of the first row (including the degree column of the polynomial)
    for elen in result:
        string_one.append(round(elen[0], 4))
    
    # creating a list for the subsequent passage through the x's
    x_col_list = []
    for col in  x_i_list:
        if col <= x_i_list[x_index]:
            x_col_list.append(col)
    
    x = Symbol('x') # for symbolic representation of x's
    
    # we go along the deltas of the first line:
    for delta in string_one:
        # we go along the column of x's
        for arg in x_col_list:
            for n in range(1, order 1):
                polynom = ( delta/(factorial(n)*h**n) )*(x - arg) # Here I stopped

CodePudding user response：

I guess you're looking for something like this:

In [52]: from sympy import symbols, prod

In [53]: x = symbols('x')

In [54]: nums = [1, 2, 3, 4]

In [55]: prod((x-n) for n in nums)
Out[55]: (x - 4)⋅(x - 3)⋅(x - 2)⋅(x - 1)

EDIT: Actually it's more efficient to do this with Mul rather than prod:

In [134]: Mul(*((x-n) for n in nums))
Out[134]: (x - 4)⋅(x - 3)⋅(x - 2)⋅(x - 1)