time complexity of nested loops - always just a multiplication of each of them seperated?-CodePudding

When looking at this code for example :

for (int i = 1; i < n; i*=2)
  for (int j = 0; j < i; j  =2)
  {
    // some contstant time operations
  }

Is it as simple as saying that because the outer loop is log and and inner loop is n , that combined the result is big(O) of nlogn ?

CodePudding user response：

Generally, we take the O time complexity to be the number of times the innermost loop is executed (and here we assume the innermost loop consists of statements of O(1) time complexity).

Consider your example. The first loop executes O(log N) times, and the second innermost loop executes O(N) times. If something O(N) is being executed O(log N) times, then yes, the final time complexity is just them multiplied: O(N log N).

Generally, this holds true with most nested loops: you can assume their big-O time complexity to be the time complexity of each loop, multiplied.

However, there are exceptions to this rule when you can consider the break statement. If the loop has the possibility of breaking out early, the time complexity will be different.

Take a look at this example I just came up with:

for(int i = 1; i <= n;   i) {
    int x = i;
    while(true) {
        x = x/2;
        if(x == 0) break;
    }
}

Well, the innermost loop is O(infinity), so can we say that the total time complexity is O(N) * O(infinity) = O(infinity)? No. In this case we know the innermost loop will always break in O(log N), giving a total O(N log N) time complexity.

CodePudding user response：

Here is the analysis of the example in the question. For simplicity I will neglect the increment of 2 in the inner loop and will consider it as 1, because in terms of complexity it does not matter - the inner loop is linear in i and the constant factor of 2 does not matter. So we can notice, that the outer loop is producing is of values which are powers of 2 capped by n, that is:

1, 2, 4, 8, ... , 2^(log2 n)

these numbers are also the numbers that the "constant time operation" in the inner loop is running for each i. So all we have to do is to sum up the above series. It is easy to see that these are geometric series:

2^0   2^1   2^2   ...   2^(log2 n)

and it has a well known solution:

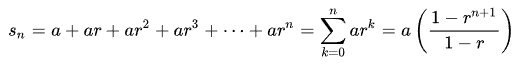
(from Wiki )

We have a=1, r=2, and... well n_from_the_image =log n. We have a same name for different variables here, so it is a bit of a problem.

Now let's substitute and get that the sum equals

(1-2^((log2 n)   1) / (1 - 2) = (1 - 2*n) / (1-2) = 2n-1

Which is a linear O(n) complexity.