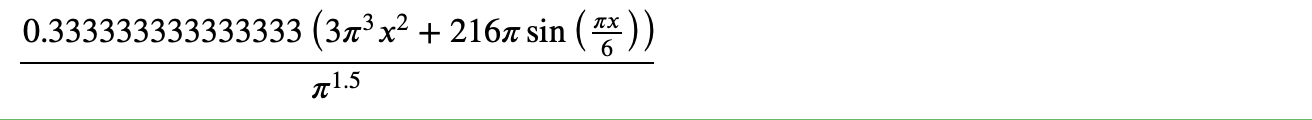Define a function that is a derivative of a function-CodePudding

I was wondering if is there is a way to define a function that is a derivative of a function. I'm new to python so I don't no much, I tired looking up stuff that might be similar but nothing has worked so far. This is what I have for my code right now.

import sympy as sp

import math 

x = sp.Symbol('x')


W = 15 #kN/m
E = 70 # Gpa
I = 52.9*10**(-6) #m**4
L = 3 #m 

e = 0.01
xi = 1.8 
y = 9


def f(x):
    return ( ( y*3*(math.pi**4)*E*I/(W*L) ) - ( 48*(L**3)*math.cos(math.pi*x/(2*L)) )   ( 48*(L**3) )   ( (math.pi**3)*(x**3) ) )/(3*L*(math.pi**3))**(1/2)

def derv(f,x):
    return sp.diff(f)

print (derv(f,x))

Also, I don't understand whatx = sp.Symbol('x') does, so if someone could explain that, that would be awesome.

Any help is appreciated.

CodePudding user response：

You've programmed the function. it appears to be a simple function of two independent variables x and y.

Could be that x = sp.Symbol('x') is how SymPy defines the independent variable x. I don't know if you need one or another one for y.

You know enough about calculus to know that you need a derivative. Do you know how to differentiate a function of a single independent variable? It helps to know the answer before you start coding.

y*3*(math.pi**4)*E*I/(W*L) ) - ( 48*(L**3)*math.cos(math.pi*x/(2*L)) )   ( 48*(L**3) )   ( (math.pi**3)*(x**3) ) )/(3*L*(math.pi**3))**(1/2)

Looks simple.

There's only one term with y in it. The partial derivative w.r.t. y leaves you with 3*(math.pi**4)*E*I/(W*L) )

There's only one term with Cx**3 in it. That's easy to differentiate: 3C*x**2.

What's so hard? What's the problem?

CodePudding user response：

In traditional programming, each function you write is translated to a series of commands that are then sent to the CPU and the result of the calculation is returned. Therefore, symbolic manipulation, like what we humans do with algebra and calculus, doesn't make any sense to the computer.

You can use sympy to find the derivative of the symbolic function returned by f() but you need to define it with the sympy versions of the cos() function (and sp.pi if you want to keep it symbolic).

For example:

import sympy as sp
    
x = sp.Symbol('x')
   
W = 15 #kN/m
E = 70 # Gpa
I = 52.9*10**(-6) #m**4
L = 3 #m 

e = 0.01
xi = 1.8 
y = 9


def f(x):
    return ( ( y*3*(sp.pi**4)*E*I/(W*L) ) - ( 48*(L**3)*sp.cos(sp.pi*x/(2*L)) )   ( 48*(L**3) )   ( (sp.pi**3)*(x**3) ) )/(3*L*(sp.pi**3))**(1/2)

def derv(f,x):
    return sp.diff(f(x)) # pass the result of f() which is a sympy function

derv(f,x)