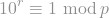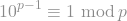I found this question online and I really have no idea what the question is even asking. I would really appreciate some help in first understanding the question, and a solution if possible. Thanks!
To see if a number is divisible by 3, you need to add up the digits of its decimal notation, and check if the sum is divisible by 3. To see if a number is divisible by 11, you need to split its decimal notation into pairs of digits (starting from the right end), add up corresponding numbers and check if the sum is divisible by 11.
For any prime p (except for 2 and 5) there exists an integer r such that a similar divisibility test exists: to check if a number is divisible by p, you need to split its decimal notation into r-tuples of digits (starting from the right end), add up these r-tuples and check whether their sum is divisible by p.
Given a prime int p, find the minimal r for which such divisibility test is valid and output it.
The input consists of a single integer p - a prime between 3 and 999983, inclusive, not equal to 5.
Example
input
3
output
1
input
11
output
2
CodePudding user response:
I have no idea how they expect a random programmer with no background to figure out the answer from this.
But here is the brief introduction to modulo arithmetic that should make this doable.
In programming, n % k is the modulo operator. It refers to taking the remainder of n / k. It satisfies the following two important properties:
(n m) % k = ((n % k) (m % k)) % k
(n * m) % k = ((n % k) * (m % k)) % k
Because of this, for any k we can think of all numbers with the same remainder as somehow being the same. The result is something called "the integers modulo k". And it satisfies most of the rules of algebra that you're used to. You have the associative property, the commutative property, distributive law, addition by 0, and multiplication by 1.
However if k is a composite number like 10, you have the unfortunate fact that 2 * 5 = 10 which means that modulo 10, 2 * 5 = 0. That's kind of a problem for division.
BUT if k = p, a prime, then things become massively easier. If (a*m) % p = (b*m) % p then ((a-b) * m) % p = 0 so (a-b) * m is divisible by p. And therefore either (a-b) or m is divisible by p.
For any non-zero remainder m, let's look at the sequence m % p, m^2 % p, m^3 % p, .... This sequence is infinitely long and can only take on p values. So we must have a repeat where, a < b and m^a % p = m^b %p. So (1 * m^a) % p = (m^(b-a) * m^a) % p. Since m doesn't divide p, m^a doesn't either, and therefore m^(b-a) % p = 1. Furthermore m^(b-a-1) % p acts just like m^(-1) = 1/m. (If you take enough math, you'll find that the non-zero remainders under multiplication is a finite group, and all the remainders forms a field. But let's ignore that.)
(I'm going to drop the % p everywhere. Just assume it is there in any calculation.)
Now let's let a be the smallest positive number such that m^a = 1. Then 1, m, m^2, ..., m^(a-1) forms a cycle of length a. For any n in 1, ..., p-1 we can form a cycle (possibly the same, possibly different) n, n*m, n*m^2, ..., n*m^(a-1). It can be shown that these cycles partition 1, 2, ..., p-1 where every number is in a cycle, and each cycle has length a. THEREFORE, a divides p-1. As a side note, since a divides p-1, we easily get 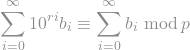
for any choice of "r-tuples of digits" b_i from { 0, ..., 10^r - 1 } (with only finitely many b_i being non-zero).
Taking b_1 = 1 and all other b_i = 0, it's easy to see that it is necessary that
It's even easier to see that this is also sufficient (all 10^ri on the left hand side simply transform into factor 1 that does nothing).
Now, if p is neither 2 nor 5, then 10 will not be divisible by p, so that Fermat's little theorem guarantees us that
, that is, at least the solution r = p - 1 exists. This might not be the smallest such r though, and computing the smallest one is hard if you don't have a quantum computer handy.
Despite it being hard in general, for very small p, you can simply use an algorithm that is linear in p (you simply look at the sequence 10, 100, 1000, 10000 ..., and stop as soon as you find something that equals 1 mod p). For example, in Scala:
def blockSize(p: Int, n: Int = 10, r: Int = 1): Int =
if n % p == 1 then r else blockSize(p, n * 10 % p, r 1)
println(blockSize(3)) // 1
println(blockSize(11)) // 2
println(blockSize(19)) // 18
or in Python:
def blockSize(p: int, n: int = 10, r: int = 1) -> int:
return r if n % p == 1 else blockSize(p, n * 10 % p, r 1)
print(blockSize(3)) # 1
print(blockSize(11)) # 2
print(blockSize(19)) # 18
A wall of numbers, just in case someone else wants to sanity-check alternative approaches:
11 -> 2
13 -> 6
17 -> 16
19 -> 18
23 -> 22
29 -> 28
31 -> 15
37 -> 3
41 -> 5
43 -> 21
47 -> 46
53 -> 13
59 -> 58
61 -> 60
67 -> 33
71 -> 35
73 -> 8
79 -> 13
83 -> 41
89 -> 44
97 -> 96
101 -> 4
103 -> 34
107 -> 53
109 -> 108
113 -> 112
127 -> 42
131 -> 130
137 -> 8
139 -> 46
149 -> 148
151 -> 75
157 -> 78
163 -> 81
167 -> 166
173 -> 43
179 -> 178
181 -> 180
191 -> 95
193 -> 192
197 -> 98
199 -> 99