Simulate multiple datasets in R, and change seed for each simulation-CodePudding

I want to generate 1 million simulated datasets and save them in a list column.

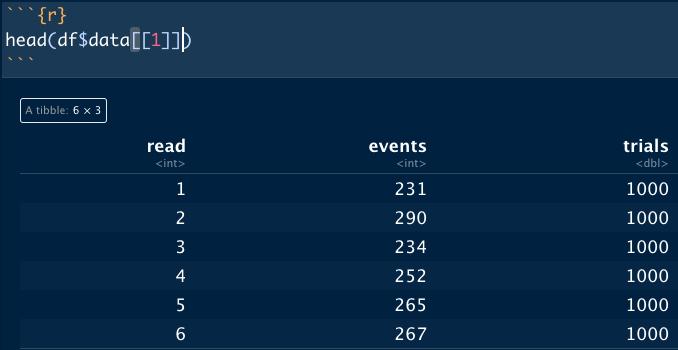
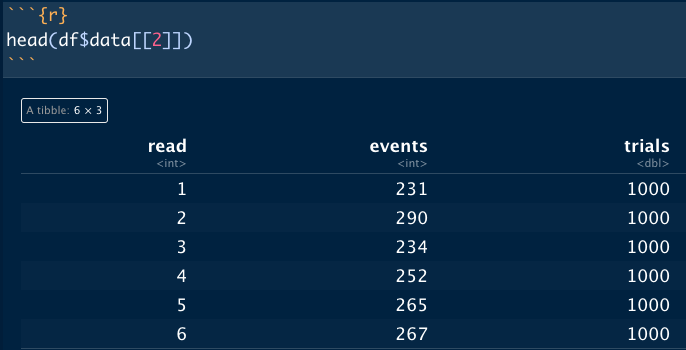
The problem I run into is that every generated dataset is identical, which I assume is a result of the operation being vectorized. Is there a way to maintain the speed of a vectorized operation while changing the seed for each execution of rbinom()?

library(tidyverse)

SIMS <- 100
df <- 
    tibble(
        sim = 1:5,
        data = 
            list(
                tibble(
                    read = 1:100,
                    events = rbinom(n=SIMS, size=1e3, prob = .25),
                    trials = 1e3
                )
        )
    )

df

head(df$data[[1]])

head(df$data[[2]])

I have tried using parallel::mclapply(), which solves the seed issue, but the performance is nowhere near as fast as the vectorized operation.

BASERATE <- .25 
DAILY_N <- 1e3
DURATION <- 500

time_to_insight <- function(){
  tibble(
    read = 1:DURATION,
    events = rbinom(n=DURATION, size=DAILY_N, prob = BASERATE),
    trials = DAILY_N
  ) 
}

temp <- 
  parallel::mclapply(
    X = 1:1000,
    FUN = time_to_insight,
    mc.cores = 8L
  )

CodePudding user response：

Depending on how your simulation works, it might be possible to create all the data for all the simulations first, and then group them into a list to get the original format with unique data.

n = 5
SIMS = 100
set.seed(42)
df <- 
  tibble(
    sim = rep(1:n, each = SIMS),
    read = rep(1:SIMS, times = n),
    events = rbinom(n=SIMS*n, size=1e3, prob = .25), 
    trials = 1e3) %>%
  nest(data = -sim)

Result

> head(df$data[[1]])
# A tibble: 6 × 3
   read events trials
  <int>  <int>  <dbl>
1     1    240   1000
2     2    262   1000
3     3    240   1000
4     4    250   1000
5     5    214   1000
6     6    244   1000
> head(df$data[[2]])
# A tibble: 6 × 3
   read events trials
  <int>  <int>  <dbl>
1     1    247   1000
2     2    260   1000
3     3    253   1000
4     4    245   1000
5     5    259   1000
6     6    247   1000

CodePudding user response：

You can (almost) maintain the speed of your original function by generating the realisations of your random variable (events) by generating all of the realisations for all of your simulations at the same time. This is possible because your event probability remains constant for all the simulations.

Here's how I would do it. First write a function to generate all your simulations at the same time.

generateTibble <- function() {
  tibble() %>% 
    expand(sim=1:5, read=1:100, trials=1000) %>% 
    mutate(events=rbinom(n=nrow(.), size=1000, prob=0.25))
}

And use it

df <- generateTibble()
df
# A tibble: 500 × 4
     sim  read trials events
   <int> <int>  <dbl>  <int>
 1     1     1   1000    246
 2     1     2   1000    232
 3     1     3   1000    258
 4     1     4   1000    233
 5     1     5   1000    259
 6     1     6   1000    251
 7     1     7   1000    254
 8     1     8   1000    263
 9     1     9   1000    267
10     1    10   1000    266
# … with 490 more rows

Demonstrate that realisations do not repeat across sims:

df %>% group_by(sim) %>% group_map(head, n=2)
[[1]]
# A tibble: 2 × 3
   read trials events
  <int>  <dbl>  <int>
1     1   1000    246
2     2   1000    232

[[2]]
# A tibble: 2 × 3
   read trials events
  <int>  <dbl>  <int>
1     1   1000    255
2     2   1000    261

[[3]]
# A tibble: 2 × 3
   read trials events
  <int>  <dbl>  <int>
1     1   1000    234
2     2   1000    239

[[4]]
# A tibble: 2 × 3
   read trials events
  <int>  <dbl>  <int>
1     1   1000    252
2     2   1000    258

[[5]]
# A tibble: 2 × 3
   read trials events
  <int>  <dbl>  <int>
1     1   1000    255
2     2   1000    258

Compare the speed of the new function with the original (faulty) version:

SIMS <- 100

originalFunction <- function() {
df <- 
  tibble(
    sim = 1:5,
    data = 
      list(
        tibble(
          read = 1:100,
          events = rbinom(n=SIMS, size=1e3, prob = .25),
          trials = 1e3
        )
      )
  )
df
}

library(microbenchmark)

microbenchmark(originalFunction, generateTibble, times=100)
Unit: nanoseconds
             expr min lq  mean median uq  max neval
 originalFunction  42 43 52.95     44 44  877   100
   generateTibble  47 48 68.14     48 54 1403   100

So, a 28% increase in mean execution time. Is that reasonable?