How should I handle music key (scale) as a feature in the knn algorithm-CodePudding

I'm doing a data science project, and I was wondering how to handle a music key (scale) as a feature in the KNN algorithm. I know KNN is based on distances, therefore giving each key a number like 1-24 doesn't make that much sense (because key number 24 is close to 1 as much as 7 close to 8). I have thought about making a column for "Major/Minor" and another for the note itself, but I'm still facing the same problem, I need to specify the note with a number, but because notes are cyclic I cannot number them linearly 1-12.

For the people that have no idea how music keys work my question is equivalent to handling states in KNN, you can't just number them linearly 1-50.

CodePudding user response：

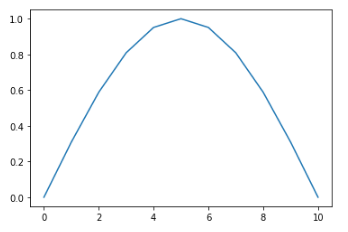
IIUC, you can convert your features to something like sin as follows. Hear I have 10 values 1-10 and I am transforming them to keep their circular relation.

a = np.around(np.sin([np.deg2rad(x*18) for x in np.array(list(range(11)))]), 3)
import matplotlib.pyplot as plt
plt.plot(a)

Output:

Through this feature engineering you can see that the circularity of your feature is encoded. The value of 0 is equal to 10.

CodePudding user response：

One way you could think about the distance between scales is to think of each scale as a 12-element binary vector where there's a 1 wherever a note is in the scale and a zero otherwise.

Then you can compute the Hamming distance between scales. The Hamming distance, for example, between a major scale and its relative minor scale should be zero because they both contain the same notes.

Here's a way you could set this up in Python

from enum import IntEnum
import numpy as np
from scipy.spatial.distance import hamming

class Note(IntEnum):
    C = 0
    Db = 1
    D = 2
    Eb = 3
    E = 4
    F = 5
    Gb = 6
    G = 7
    Ab = 8
    A = 9
    Bb = 10
    B = 11

major = np.array((1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1))
minor = np.array((1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0)) #WHWWHWW Natural Minor

# Transpose the basic scale form to a key using Numpy's `roll` function

cMaj = np.roll(major, Note.C) # Rolling by zero changes nothing
aMin = np.roll(minor, Note.A)
gMaj = np.roll(major, Note.G)
fMaj = np.roll(major, Note.F)

print('Distance from cMaj to aMin', hamming(cMaj, aMin))
print('Distance from cMaj to gMaj', hamming(cMaj, gMaj)) # One step clockwise on circle of fifths
print('Distance from cMaj to fMaj', hamming(cMaj, fMaj)) # One step counter-clockwise on circle of fifths