Why is my rotation matrix not working properly?-CodePudding

I've been working a bit on this simple rasterizer, but the cube I imported is not rotating properly. Here's a picture of the issue:

I copied a rotation matrix from this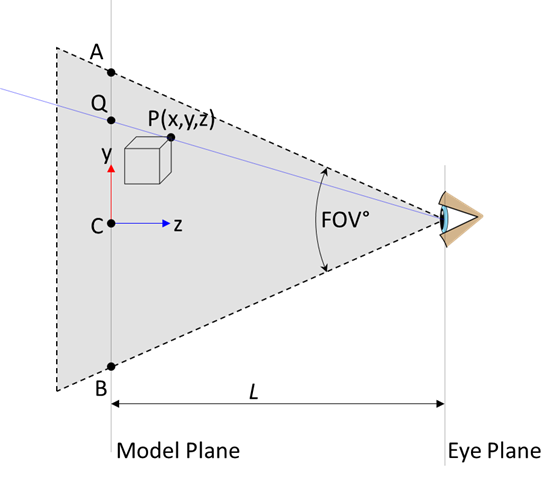

Given a point P with (x,y,z) coordinates, you want to find point Q which is the projection on the model plane.

More specifically you need to find the distance QC and relate it as a ratio to the distance AB. This is because on screen the distance AB corresponds to the height H in pixels of your viewport.

So the vertical pixel count is

          y     L
py = H * --- * ---
         AB    L-z

where L is the distance to the camera/eye along the z axis.

Sometimes the model size AB isn't known, but instead the field of view (FOV) in degrees is. From trigonometry, we have tan(fov/2*π/180) = AB/(2*L) which simplifies the projection as such

                 1          y
py = H * -------------- *  ---
         tan(fov*π/360)    L-z

Typically the factor f=H/tan(fov*π/360) is pre-computed and the projection of point P is

px = f * (x/(L-z))
py = f * (y/(L-z))

CodePudding user response：

It ended up being an issue with my perspective projection. This is the code that worked for me:

pub fn perspective(vec: Vec3, camPos: Vec3, fov: f32) -> Vec2 {

    let camDist = Vec3::length(camPos - vec);
    let pixel_x = fov*vec.x/(camDist-vec.z);
    let pixel_y = fov*vec.y/(camDist-vec.z);
    return Vec2::new(pixel_x, pixel_y);
}

Credit to @JohnAlexiou for the massive help.