How to occupy a 10 by 10 block with 2 * 3 blocks that doesn't let others to push another 2 * 3-CodePudding

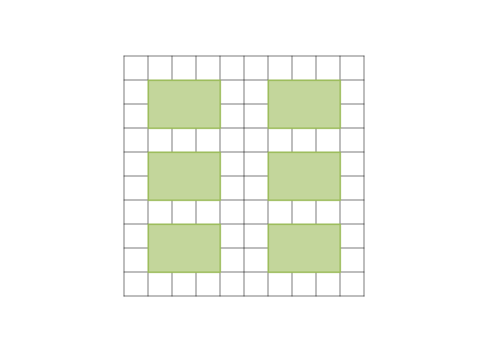
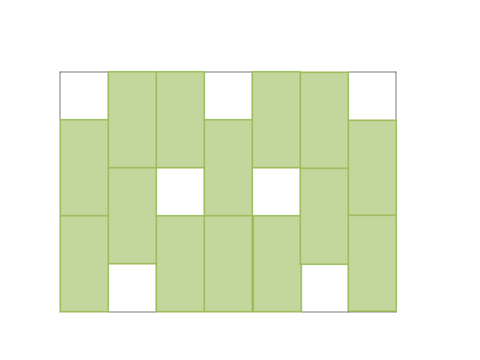
I want to find out the minimum number of 2 * 3 blocks that I can fill in 100 pixels that don't allow any other 2 * 3 blocks to fill in like the below picture.

2 * 3 in 10 * 10 = 6

or another example:

2 * 1 in 5 * 7 = 14

I've searched a lot but I've not been successful so far. I do not want any code but I want the algorithm name or any advice to find my way.

any help would be highly appreciated.

CodePudding user response：

From the comments I understood, that we can't rotate rectangles. So then we use the following approach:

Imagine, you want to solve the same problem, but only for the line, where rect size is 1xRectW in 1xGridW grid.

I will use "X" for rect cell, "0" for empty cell. Example has 1x3 rect and 1x10 grid.

From the left side I can leave empty (RectW - 1) cells at max:

00XXX00000

Then I can leave empty (RectW - 1) cells at max from the previous’s rect right side:

00XXX00XXX

Now I let's add another dimension. Let's say we have 2 rows. I can keep using the same logic here, but instead of copying rectangle, I will copy the whole first row:

00XXX00XXX
00XXX00XXX

Now we want to do the same for 2x4 rectangle in 10x11 grid. Here we got rectangle of height 2, so we will use 2 rows for the first step:

000XXXXXXXX
000XXXXXXXX

And extend it for rows:

00000000000
000XXXXXXXX
000XXXXXXXX
00000000000
000XXXXXXXX
000XXXXXXXX
00000000000
000XXXXXXXX
000XXXXXXXX
00000000000

As you can notice, we add extra (RectH - 1) on the top.

If you will pay attention, you will see, that actually we are just performing division with rounding.

So in python we can express this idea with mathematical abstraction like this:

def solver(rectH, rectW, gridH, gridW) -> int:
    w = round(gridW / (rectW * 2 - 1))
    h = round(gridH / (rectH * 2 - 1))
    return w * h

Results:

>>> solver(2, 3, 10, 10)
6
>>> solver(2, 1, 5, 7)
14