Splitting Images into Individual Pixels/Blocks Python-CodePudding

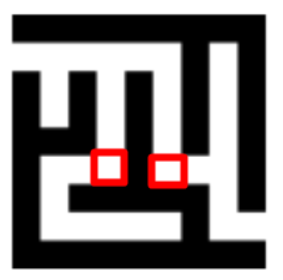
I would like to create or find an algorithm that turns mazes like the ones attached, into an array in a list. All the black spaces can become a string, 'w' and all the white spaces can become 'b'. Example (example is just a basic display, no maze):

    self.base_map = [
      ['w', 'w', 'w', 'w', 'w', 'w', 'w', 'w', 'w', 'w'],
      ['w', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b','w'],
      ['w', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b','w'],
      ['w', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b','w'],
      ['w', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b','w'],
      ['w', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b','w'],
      ['w', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b','w'],
      ['w', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b','w'],
      ['w', 'w', 'w', 'w', 'w', 'w', 'w', 'w', 'w', 'w']
    ]

I think this can be done by splitting the image into blocks (attached) and scanning each one to see its color. I'm not sure though. If it helps, each of the mazes is 9x9, each block being 1.

Is there a library and algorithm that can help me here?

CodePudding user response：

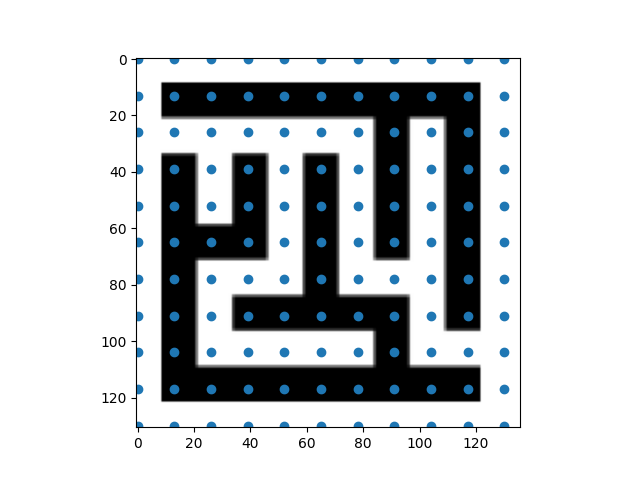
Your image has a variable width of walls, so the point grid is not perfect, but here you have the general idea.

You can just read the colors of the image, and round them to 0 (black), or 1 (white), to detect empty spaces and walls.

This code does not detects the number of rows and columns (I counted them and hardcoded 10 columns and 10 rows)

import numpy as np
import cv2
import matplotlib.pyplot as plt


def downloadImage(URL):
    """Downloads the image on the URL, and convers to cv2 RGB format"""
    from io import BytesIO
    from PIL import Image as PIL_Image
    import requests

    response = requests.get(URL)
    image = PIL_Image.open(BytesIO(response.content))
    return cv2.cvtColor(np.array(image), cv2.COLOR_BGR2RGB)


URL = "https://i.stack.imgur.com/wm8dr.png"

img = downloadImage(URL)


plt.imshow(img)
x, y = [], []
columns = 10
rows = 10
stepY, stepX = img.shape[0]//rows, img.shape[1]//columns
xrange = range(0, img.shape[0], stepX)
yrange = range(0, img.shape[1], stepY)
mazeElement = {0: 'b', 1: '█'}
for r in yrange:
    for c in xrange:
        x.append(c)
        y.append(r)

plt.scatter(x, y)
plt.show()

base_map = [[mazeElement[round(sum(img[r, c][:])/3//255, 0)]
            for c in xrange] for r in yrange]
print(*["".join(row) for row in base_map], sep='\n')

it prints

███████████
█bbbbbbbbb█
███████b█b█
█b█b█b█b█b█
█b█b█b█b█b█
█bbb█b█b█b█
█b█bbbbb█b█
█b█████b███
█bbbbbbbbb█
███████████

CodePudding user response：

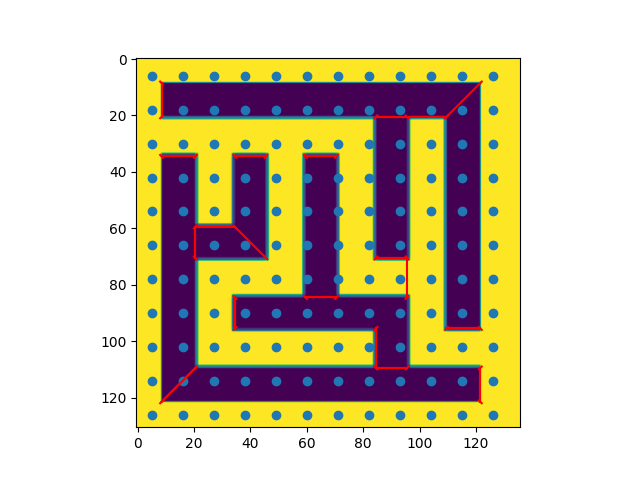
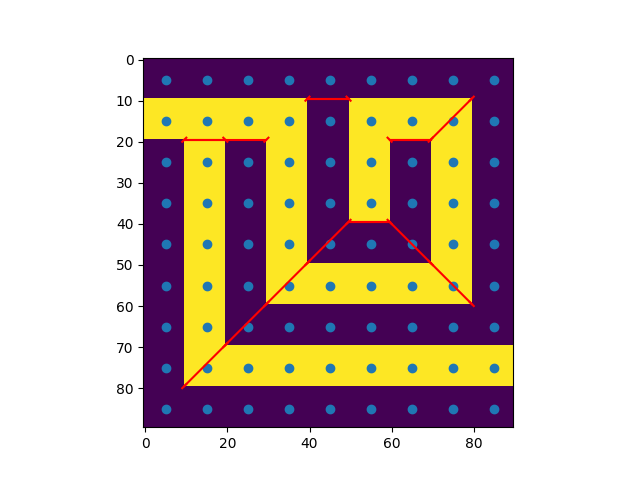
This algorithm autodetects the width of the walls and halls (assuming they are equal), but fails anyways, because the walls on the images do not have constant width.

Maybe is possible to adjust the coefficients by some linear regression.

The autodetection works by identifying the corners, and calculating the distances between closest corners.

import numpy as np
import cv2
import matplotlib.pyplot as plt


def downloadImage(URL):
    """Downloads the image on the URL, and convers to cv2 RGB format"""
    from io import BytesIO
    from PIL import Image as PIL_Image
    import requests

    response = requests.get(URL)
    image = PIL_Image.open(BytesIO(response.content))
    return cv2.cvtColor(np.array(image), cv2.COLOR_BGR2RGB)


URL = "https://i.stack.imgur.com/wm8dr.png"

img = downloadImage(URL)

# Convert ot 2 color
img = cv2.cvtColor(np.array(img), cv2.COLOR_BGR2GRAY)
ret3, th3 = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY)
# plt.imshow(th3, cmap='gray')

# Detect corners
CornerKernel = np.ones((3, 3), np.uint8)
corner = cv2.filter2D(th3//255, -1, CornerKernel)
# A corner add up to to 1 or 9
Corners = np.argwhere((corner == 4) | (corner == 8))
antiCorners = np.argwhere((corner == 1) | (corner == 5))
# for each point in Corners, find the closet point in antiCorners
Corner_antiCorner = []
for point in Corners:
    distances = np.linalg.norm(antiCorners-point, axis=1)
    closest = antiCorners[np.argmin(distances)]
    Corner_antiCorner.append((point closest)/2)
    plt.plot([point[1], closest[1]], [point[0], closest[0]], color='r')
# For eachpoint in Corner_antiCorner, find the closet point in Corner_antiCorner
closestCorners = []
for point in Corner_antiCorner:
    distances = np.linalg.norm(Corner_antiCorner-point, axis=1)
    # closest is itself, so second closest is chosen
    closest = Corner_antiCorner[distances.argsort()[1]]
    closestCorners.append((point, closest))
    plt.plot([point[1], closest[1]], [point[0], closest[0]], color='r')

# Sample of separations dx,dy
dx = np.array([abs(p[1]-q[1]) for p, q in closestCorners])
dy = np.array([abs(p[0]-q[0]) for p, q in closestCorners])

mediandx = np.median(dx[dx > 0])
mediandy = np.median(dy[dy > 0])

# plt.scatter([p[1] for p in corners],[p[0] for p in corners])
# plt.scatter([p[1] for p in antiCorners],[p[0] for p in antiCorners])
plt.imshow(img)

stepY, stepX = int(mediandy), int(mediandx)
xrange = range(stepX//2, img.shape[0], stepX)
yrange = range(stepY//2, img.shape[1], stepY)
x, y = [], []
mazeElement = {0: 'b', 1: '█'}
for r in yrange:
    for c in xrange:
        x.append(c)
        y.append(r)

plt.scatter(x, y)
plt.show()

base_map = [[mazeElement[img[r, c]//255]
            for c in xrange if c < img.shape[1]] for r in yrange if r < img.shape[0]]
print(*["".join(row) for row in base_map], sep='\n')

████████████
█bbbbbbbbbb█
████████b█b█
█b█b█bb█b█b█
█b█b█bb█b█b█
█bbb█bb█b█b█
█b███bb███b█
█b█bbbbbb█b█
█b██████b███
█bbbbbbbbbb█
████████████

bbbbbbbbb
████b███b
b█b█b█b█b
b█b█b█b█b
b█b█bbb█b
b█b█████b
b█bbbbbbb
b████████
bbbbbbbbb