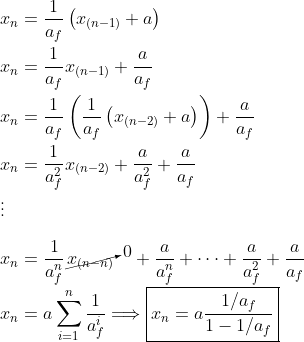I am developing a game and I have an object with a horizontal speed. When moving, it has a relatively high acceleration rate.

I made a small example to illustrate what I'm struggling with:

This is how I got the square to accelerate. At the very start of the program, it defines four variables.

// position of the square
let pos_x = 100

// speed of the square
let speed_x = 0

// speed at which the square accelerates
let accel_speed = .06

// the amount the square slows down
let friction = 1.005

Then, in the update function (a function that runs once every frame), it does the following calculations to the square:

// add the speed to the position
pos_x  = speed_x

// make the x speed accelerate
speed_x  = accel_speed

// slow the x speed down by the friction
speed_x /= friction

The great thing about this technique is things can accelerate, but not eternally. Because I applied friction to the square (i.e. dividing it by a very small amount each time), it means that the faster the square gets, the slower it will accelerate.

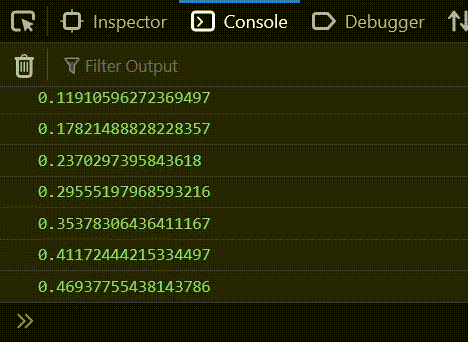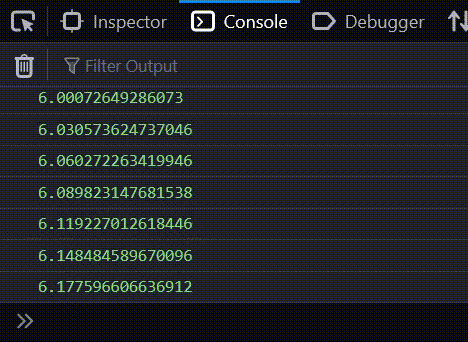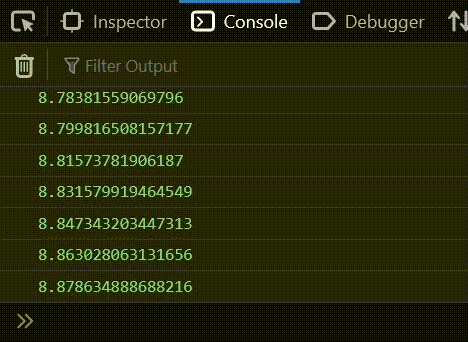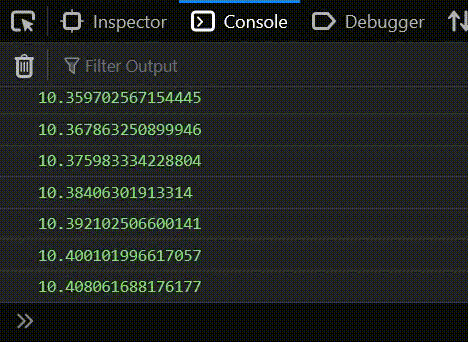
I logged the speed to the console and you will see it starts to slow down around the 10 mark:

So now here's my question: I have the friction, I have the acceleration speed, and I want to know the maximum speed of the square. Beacause the square's acceleration is constantly slowing down, there will be a point when JavaScript runs out of decimal places and the speed becomes constant.

For example, after watching the console for a long time, the settling point turned out to be 12.000000000000178. How would I find this number just with maths - just by using the friction and acceleration variables? How can I figure out the square's final speed when it's acceleration finally stops?

I hope you understand my question.

Thanks

CodePudding user response：

To find the maximum velocity of a moving object, you can divide its speed by the damping. In your case, you might write the following.

accel_speed / (friction - 1)

CodePudding user response：

It starts as a recurrence and then boils down to a classic infinite geometric progression.

The problem with recurrence is finding a closed form of this relation. Think of it as a recursion in programming terms: you must define a base case and the general case.

Let x_n be the nth speed of the square, base case is when x₀ = 0. And consider constants a_f the friction value and a the acceleration.

Some math later...

The infinite formula appeared with only constant terms a and a_f. Thus, replacing values yields x_n = 12.

It will never be strictly equal to 12 because it must run forever, but after some long time, it will be closer enough to that number that you may think it is stable.