Custom Operations on Multi-dimensional Tensors-CodePudding

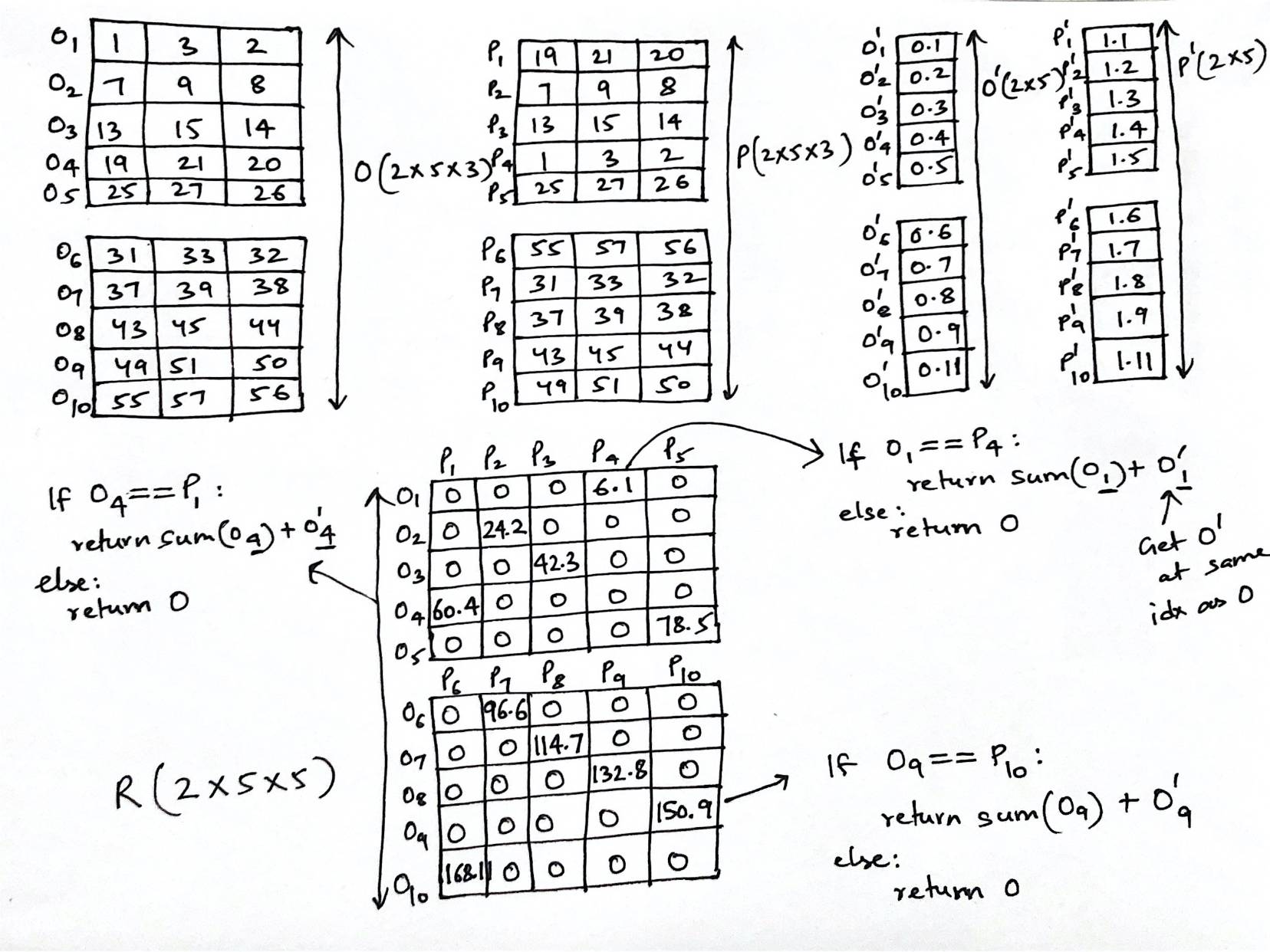
I am trying to compute the tensor R (see image) and the only way I could explain what I am trying to compute is by doing it on a paper:

o = torch.tensor([[[1, 3, 2], [7, 9, 8], [13, 15, 14], [19, 21, 20], [25, 27, 26]], [[31, 33, 32], [37, 39, 38], [43, 45, 44], [49, 51, 50], [55, 57, 56]]])
p = torch.tensor([[[19, 21, 20], [7, 9, 8], [13, 15, 14], [1, 3, 2], [25, 27, 26]], [[55, 57, 56], [31, 33, 32], [37, 39, 38], [43, 45, 44], [49, 51, 50]]])

# this is O' in image
o_prime = torch.tensor([[0.1, 0.2, 0.3, 0.4, 0.5], [0.6, 0.7, 0.8, 0.9, 0.11]])

# this is P' in image
p_prime = torch.tensor([[1.1, 1.2, 1.3, 1.4, 1.5], [1.6, 1.7, 1.8, 1.9, 1.11]])

# this is R (this is what I need)
r = torch.tensor([[[0, 0, 0, 6.1, 0], [0, 24.2, 0, 0, 0], [0, 0, 42.3, 0, 0], [60.4, 0, 0, 0, 0], [0, 0, 0, 0, 78.5]], [[0, 96.6, 0, 0, 0], [0, 0, 114.7, 0, 0], [0, 0, 0, 132.8, 0], [0, 0, 0, 0, 150.9], [168.11, 0, 0, 0, 0]]])

How do I get R without looping over tensors?

correction: In the image, I forgot to add value of p' along with sum(o) o'

CodePudding user response：

You can construct a helper tensor containing the resulting values sum(o) o' p':

>>> v = o.sum(2, True)   o_prime[...,None]   o_prime[...,None]
tensor([[[  7.2000],
         [ 25.4000],
         [ 43.6000],
         [ 61.8000],
         [ 80.0000]],

        [[ 98.2000],
         [116.4000],
         [134.6000],
         [152.8000],
         [169.2200]]])

Then you can assemble a mask for the final tensor via broadcasting:

>>> eq = o[:,None] == p[:,:,None]

Ensuring all three elements on the last dimension match:

>>> eq.all(dim=-1)
tensor([[[False, False, False,  True, False],
         [False,  True, False, False, False],
         [False, False,  True, False, False],
         [ True, False, False, False, False],
         [False, False, False, False,  True]],

        [[False, False, False, False,  True],
         [ True, False, False, False, False],
         [False,  True, False, False, False],
         [False, False,  True, False, False],
         [False, False, False,  True, False]]])

Finally, you can simply multiply both tensor and auto-broadcasting will handle the rest:

>>> R = eq.all(dim=-1) * v
tensor([[[  0.0000,   0.0000,   0.0000,   7.2000,   0.0000],
         [  0.0000,  25.4000,   0.0000,   0.0000,   0.0000],
         [  0.0000,   0.0000,  43.6000,   0.0000,   0.0000],
         [ 61.8000,   0.0000,   0.0000,   0.0000,   0.0000],
         [  0.0000,   0.0000,   0.0000,   0.0000,  80.0000]],

        [[  0.0000,   0.0000,   0.0000,   0.0000,  98.2000],
         [116.4000,   0.0000,   0.0000,   0.0000,   0.0000],
         [  0.0000, 134.6000,   0.0000,   0.0000,   0.0000],
         [  0.0000,   0.0000, 152.8000,   0.0000,   0.0000],
         [  0.0000,   0.0000,   0.0000, 169.2200,   0.0000]]])

CodePudding user response：

You can compute a mask (2,5,5) that tells you where o_i==p_j:

mask = (o.repeat(1,1,p.shape[1]).reshape(o.shape[0],o.shape[1],p.shape[1],o.shape[2])==p.reshape(p.shape[0],1,p.shape[1],p.shape[2])).all(-1)

mask is:

tensor([[[False, False, False,  True, False],
         [False,  True, False, False, False],
         [False, False,  True, False, False],
         [ True, False, False, False, False],
         [False, False, False, False,  True]],

        [[False,  True, False, False, False],
         [False, False,  True, False, False],
         [False, False, False,  True, False],
         [False, False, False, False,  True],
         [ True, False, False, False, False]]])

then you can compute the indices like:

ids = torch.argwhere(mask)

ids tells you which element of o and p consider for the equation:

tensor([[0, 0, 3],
        [0, 1, 1],
        [0, 2, 2],
        [0, 3, 0],
        [0, 4, 4],
        [1, 0, 1],
        [1, 1, 2],
        [1, 2, 3],
        [1, 3, 4],
        [1, 4, 0]])

Finally you can defy R = torch.zeros(mask.shape) and fill it with the equation:

R[mask] = o[ids[:,0], ids[:,1]].sum(1) o_prime[ids[:,0], ids[:,1]] p_prime[[ids[:,0], ids[:,1]]]

output R is:

tensor([[[  0.0000,   0.0000,   0.0000,   7.2000,   0.0000],
         [  0.0000,  25.4000,   0.0000,   0.0000,   0.0000],
         [  0.0000,   0.0000,  43.6000,   0.0000,   0.0000],
         [ 61.8000,   0.0000,   0.0000,   0.0000,   0.0000],
         [  0.0000,   0.0000,   0.0000,   0.0000,  80.0000]],

        [[  0.0000,  98.2000,   0.0000,   0.0000,   0.0000],
         [  0.0000,   0.0000, 116.4000,   0.0000,   0.0000],
         [  0.0000,   0.0000,   0.0000, 134.6000,   0.0000],
         [  0.0000,   0.0000,   0.0000,   0.0000, 152.8000],
         [169.2200,   0.0000,   0.0000,   0.0000,   0.0000]]])