Efficiently compute a sum based on sequences in R-CodePudding

I'm trying to compute a specific sum in R as quickly as possible. The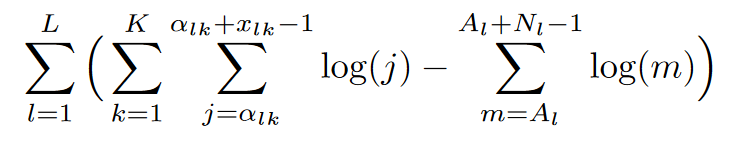

and the relevant input objects are two L times K matrices x (contains only positive integers) and alpha (contains only positive real values). A is equivalent to rowSums(alpha) and N is equivalent to rowSums(x). Subscripts l and k denote a row / a column of alpha or x, respectively.

At first I thought it's going to be easy to come up with something that's super-quick, but I couldn't find an elegant solution. I think a matrix-valued version of seq() would be very helpful here. Does anyone have a creative solution to implement this efficiently?

Here's an easy-to-read, but obviously inefficient, loop-based version for reference:

# parameters
L = 20
K = 5

# x ... L x K matrix of integers
x = matrix(1 : (L * K), L, K)

# alpha ... L x K matrix of positive real numbers
alpha = matrix(1 : (L * K) / 100, L, K)

# N ... sum over rows of x
N = rowSums(x)

# A ... sum over rows of alpha
A = rowSums(alpha)


# implementation 

stacksum = function(x, alpha, N, A){
  
  # parameters
  K = ncol(x)
  L = nrow(x)
  
  result = 0
  
  for(ll in 1:L){
  
  # first part of sum
  first.sum = 0
  
  for(kk in 1:K){
    
    # create sequence
    sequence.k = seq(alpha[ll, kk], (alpha[ll, kk]   x[ll, kk] - 1), 1)
    
    # take logs and sum
    first.sum = first.sum   sum(log(sequence.k))
    
  }
  
  # second part of sum
  second.sum = sum(log(seq(A[ll], (A[ll]   N[ll] - 1), 1)))
  
  # add to result
  result = result   first.sum - second.sum
  
  }
  
  return(result)
  
  
}

# test
stacksum(x, alpha, N, A)

CodePudding user response：

Update with a lgamma solution based on @RobertDodier comments.

Using sequence and rep.int.

# parameters
L <- 20
K <- 5

# x ... L x K matrix of integers
x <- matrix(1 : (L * K), L, K)
# alpha ... L x K matrix of positive real numbers
alpha <- matrix(1 : (L * K) / 100, L, K)
# N ... sum over rows of x
N <- rowSums(x)
# A ... sum over rows of alpha
A <- rowSums(alpha)

# proposed solution
stacksum2 <- function(x, alpha, N, A) {
  sum(log(sequence(x, alpha)   rep.int(alpha %% 1, x))) - sum(log(sequence(N, A)   rep.int(A %% 1, N)))
}

# solution from Robert Dodier's comments
stacksum3 <- function(x, alpha, N, A) {
  sum(lgamma(alpha   x) - lgamma(alpha)) - sum(lgamma(A   N) - lgamma(A))
}

# OP solution
stacksum1 = function(x, alpha, N, A){
  # parameters
  K = ncol(x)
  L = nrow(x)
  result = 0
  
  for(ll in 1:L){
    # first part of sum
    first.sum = 0
    for(kk in 1:K){
      # create sequence
      sequence.k = seq(alpha[ll, kk], (alpha[ll, kk]   x[ll, kk] - 1), 1)
      # take logs and sum
      first.sum = first.sum   sum(log(sequence.k))
    }
    # second part of sum
    second.sum = sum(log(seq(A[ll], (A[ll]   N[ll] - 1), 1)))
    # add to result
    result = result   first.sum - second.sum
  }
  result
}

microbenchmark::microbenchmark(stacksum1 = stacksum1(x, alpha, N, A),
                               stacksum2 = stacksum2(x, alpha, N, A),
                               stacksum3 = stacksum3(x, alpha, N, A),
                               check = "equal")
#> Unit: microseconds
#>       expr      min        lq       mean    median        uq      max neval
#>  stacksum1 1696.700 1751.3015 1966.92793 1793.0510 2086.4510 4690.401   100
#>  stacksum2  235.402  242.1505  288.93490  248.7000  266.0505 3612.901   100
#>  stacksum3   18.101   19.0510   45.71009   20.1015   22.5010 2498.901   100