I need to generate some random weights for multiple runs, each one different by the previous one, while having some specific constrains:

Sum = 100
There are constraints about the min and max value of each item in the list

ranges = [range(0,10), range(10,20), range(50,70), range(0,20)]

One of the solutions is [0,20,60,20] for example, or [0,20,65,15].

What's the most performing way for getting a random solution from my ranges?

That's my current brute-forcing code, but it obviously explodes when ranges becomes too big (I think I'll have 50 constraints at most).

tot = 100
res = []
for vector in itertools.product(*ranges):
    if sum(vector) == tot:
          res.append(vector)
    if res:
        final_combo = random.choice(res)

CodePudding user response：

The following function will pick one item from each range such that the sum of all items equals the given total. Since the given total might bias the choices of items towards either end of the ranges (like for your example), the sequence of ranges is first randomized in order to distribute this bias equally over all sequences.

import random

def generate(ranges, *, total=100):
    # Shuffle the ranges to distribute the bias induced by `total`.
    indices = random.sample(range(len(ranges)), k=len(ranges))
    ranges = [ranges[i] for i in indices]

    lb = [r.start for r in ranges]
    ub = [r.stop-1 for r in ranges]
    if sum(lb) > total:
        raise ValueError('Sum of lower boundaries is greater than total')
    if sum(ub) < total:
        raise ValueError('Sum of upper boundaries is less than total')

    vec = []
    for i, r in enumerate(ranges[:-1]):
        start = max(r.start, total - sum(ub[i 1:]))
        stop = min(r.stop, total - sum(lb[i 1:])   1)
        x = random.choice(range(start, stop))
        total -= x
        vec.append(x)
    assert total in ranges[-1]
    vec.append(total)

    vec = [x for _,x in sorted(zip(indices, vec))]  # undo the shuffling
    return vec

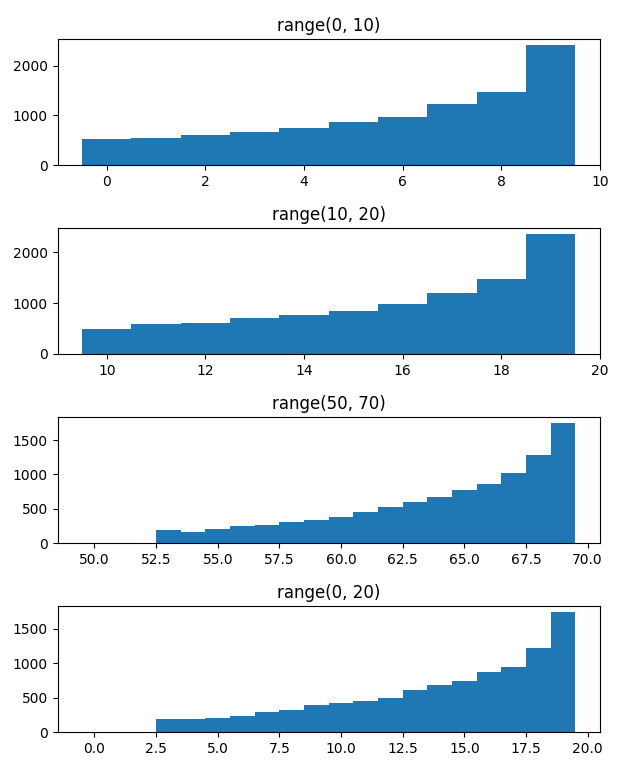
The following code plots the samples generated by this function:

import matplotlib.pyplot as plt
import numpy as np

ranges = [range(0,10), range(10,20), range(50,70), range(0,20)]
random.seed(0)

samples = np.stack([generate(ranges) for _ in range(10**4)])

fig, axes = plt.subplots(nrows=len(ranges), figsize=(7, 9))
for s, r, ax in zip(samples.T, ranges, axes):
    ax.set(title=f'{r!s}')
    ax.hist(s, bins=[*(i-0.5 for i in r), r.stop-0.5])
plt.subplots_adjust(hspace=0.5)
plt.show()

Here it can be seen that the distributions are biased towards their upper boundary since the total 100 is greater than the sum of averages of all ranges:

CodePudding user response：

weight = [A, B, C, D],

0 <= A <= 10
10 <= B <= 20
50 <= C <= 70
0 <= D <= 20
A B C D = 100

We can change it in to these constraints by letting B = B' 10 and C = C' 50

0 <= A <= 10
0 <= B' <= 10
0 <= C <= 20
0 <= D <= 20
A B' C' D = 40

Although they can be any number in the range, one of them should be limited because their sum is determined.
(Degree of Freedom = 3)

A and B' are from 0 to 10, C' and D are from 0 to 20.

What should we determine first?

Suppose C' D is lower than 20, which means A B' = 40 - (C' D) should be greater than 20.

Then, there's a contradiction. (A B' <= 20)

Thus, we must determine A and B' first.

-> Pick A first(A = rand from 0 to 10)
-> Pick B' second(B' = rand from 0 to 10)
-> Pick C' third(C' = rand from max(0, 20-(A B') to 20)
-> Evaluate D(D = 40-(A B' C')

Now, all you have to do is sum 10 to B' and 50 to C' and make it into code.

CodePudding user response：

This is the randomest constructed way possible I can think of.

import random

ranges = [range(0, 10), range(10, 20), range(50, 70), range(0, 20)]
total = 100

# Initialize an output list with the first constraint for each element (x = min).
answer = [r.start for r in ranges]

# Find out the maximum each element in the list can take.
max_to_add = [r.stop - r.start - 1 for r in ranges]

# Some sanity checks.
if sum(answer) > total:
    raise RuntimeError("The ranges have too high start values that collectively exceed the total")

if sum(answer)   sum(max_to_add) < total:
    raise RuntimeError("The ranges can never make up the total")

# Keep trying till we satisfy the sum constraint.
while total != sum(answer):
    # Get a random index in the list to add on.
    i = random.randint(0, len(max_to_add) - 1)
    # Get a random number that doesn't break our constraint (x < max).
    random_to_add = random.randint(0, max_to_add[i])
    # Make sure the random we choose doesn't make us go past the total sum.
    random_to_add = min(random_to_add, total - sum(answer))
    # Update the constraint for that element.
    max_to_add[i] -= random_to_add
    # Add the random number to the element.
    answer[i]  = random_to_add

print("Random list:", answer)
print("Total sum:", sum(answer))

You can see this code will struggle when the ranges tightly make up to the total number or a little bit more:

# Try raising total to 10000 for example and it will struggle more.
total = 100
# With these ranges we should get answer list of [1, 1, ...., 1] due to the constraints we have.
ranges = [range(0, 2)] * total

One possible solution for this is to store another list of indices that can be added to and use random.choice to pick from it (instead of random.randint(0, len(max_to_add) - 1))

Update:

This is the version for considering only the elements we can actually add to:

import random

ranges = [range(0, 10), range(10, 20), range(50, 70), range(0, 20)]
total = 100

# Initialize an output list with the first constraint for each element (x = min).
answer = [r.start for r in ranges]

# Find out the maximum each element in the list can take.
max_to_add = [r.stop - r.start - 1 for r in ranges]
still_can_add_to = list(range(len(max_to_add)))

# Some sanity checks.
if sum(answer) > total:
    raise RuntimeError("The ranges have too high start values that collectively exceed the total")

if sum(answer)   sum(max_to_add) < total:
    raise RuntimeError("The ranges can never make up the total")

# Keep trying till we satisfy the sum constraint.
while total != sum(answer):
    # Get a random index in the list to add on.
    i = random.choice(still_can_add_to)
    # Get a random number that doesn't break our constraint (x < max).
    random_to_add = random.randint(0, max_to_add[i])
    # Make sure the random we choose doesn't make us go past the total sum.
    random_to_add = min(random_to_add, total - sum(answer))
    # Update the constraint for that element.
    max_to_add[i] -= random_to_add
    # Remove this element from the list of actively checked elements that we add to.
    if max_to_add[i] == 0:
        still_can_add_to.remove(i)
    # Add the random number to the element.
    answer[i]  = random_to_add

print("Random list:", answer)
print("Total sum:", sum(answer))

This is an optimization that shines in cases when the ranges tightly make up to the total number:

total = 10000
# With these ranges we should get answer list of [1, 1, ...., 1] due to the constraints we have.
ranges = [range(0, 2)] * total

In the example above, the updated version takes about 3s whereas the old one takes about 13s.