Fastest way to compute a rolling distance between high-dimensional vectors in numpy?-CodePudding

I have a time series of vectors: Y = [v1, v2, ..., vn]. At each time t, I want to compute the distance between vector t and the average of the vectors before t. So for example, at t=3 I want to compute the cosine distance between v3 and (v1 v2)/2.

I have a script to do it but wondering if there's any way to do this faster via numpy's convolve feature or something like that?

import numpy
from scipy.spatial.distance import cosine
np.random.seed(10)

# Generate `T` vectors of dimension `vector_dim`
# NOTE: In practice, the vector is a very large column vector! 
T = 3
vector_dim = 2
y = [np.random.rand(1, vector_dim)[0] for t in range(T)]


def moving_distance(v):
  moving_dists = []
  for t in range(len(v)):
    if t == 0: 
      pass
    else:
      # Create moving average of values up until time t
      prior_vals = v[:t]
      m_avg = np.add.reduce(prior_vals) / len(prior_vals) 
      # Now compute distance between this moving average and vector t
      moving_dists.append(cosine(m_avg, v[t]))
  return moving_dists

d = moving_distance(y)

For this dataset, it should return: [0.3337342770170698, 0.0029993196890111262]

CodePudding user response：

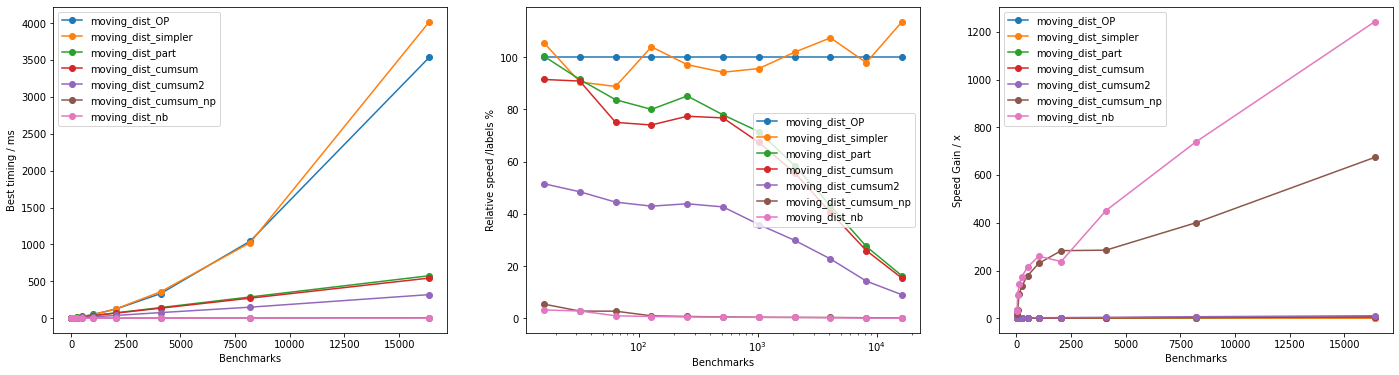
These results indicate that Numba approach is the fastest by far and large, but the vectorized approach is reasonably fast. When it comes to explicit non-accelerated looping, it is still beneficial to use the custom-defined cos_dist() in place of scipy.spatial.distance.cosine() (see moving_dist_cumsum() vs moving_dist_cumsum2()), while np.cumsum() is reasonably faster than np.add.reduce() but only marginally faster over computing the partial sum. Finally, moving_dist_OP() and moving_dist_simpler() are effectively equivalent (as expected).