Limit maximum df of smooth in ggplot?-CodePudding

Firstly, I am very new to R, very basic statistical knowledge and have thus been winging it when it comes to my analysis. This means googling the coding I need for the results, and due to how small some samples are I will have to check if they are of any statistical relevance later. For now, though, I'm just trying to reach my goal of displaying graphs on the screen.

I have two datasets I want to run gams for - one with 9 obs. of 22 variables, the other with 4 obs. of 22 variables (both filtered from a source table of 44 obs. of 22 variables). Example:

Flight_Dur    Distance
 429            2396
 59.2           1096
 26.6           1174

I'm plotting the linear GAMM with mgcv with this code:

GAMM_Plot <- gam(Flight_Dur ~ s(Distance, k = 4), data = my_table, method = "REML")

Since I was getting the error message "A term has fewer unique covariate combinations than specified maximum degrees of freedom", I followed this guide and added k = [number of objects I have], so 4 for one dataset and 9 for the other, to limit my df. Agsin, I don't know what it does to the relevance of my results, I'm just trying to make the graphs work for now.

To visualise scatterplots along with the lines, however, I used:

GAMM_Plot2 <- ggplot(my_table, aes(x=Distance, y=Flight_Dur))   
  geom_point() 
  geom_smooth(method=gam)

Interestingly, plotting the latter won't give me an error message, however both graphs are clearly different since the second one has no limitation set for df. I would like to set this limitation for the ggplot code as well - how would this be possible?

Thank you.

CodePudding user response：

You can specify the method to use mgcv::gam and the formula including k = 4.

my_table <- data.frame(
  Flight_Dur = c(429, 59.2, 26.6, 30),
  Distance = c(2396, 1096, 1174, 1000)
)

library(ggplot2)
library(mgcv)
#> Loading required package: nlme
#> This is mgcv 1.8-33. For overview type 'help("mgcv-package")'.

ggplot(my_table, aes(x=Distance, y=Flight_Dur))   
  geom_point() 
  geom_smooth(method = mgcv::gam, formula = y ~ s(x, k = 4))

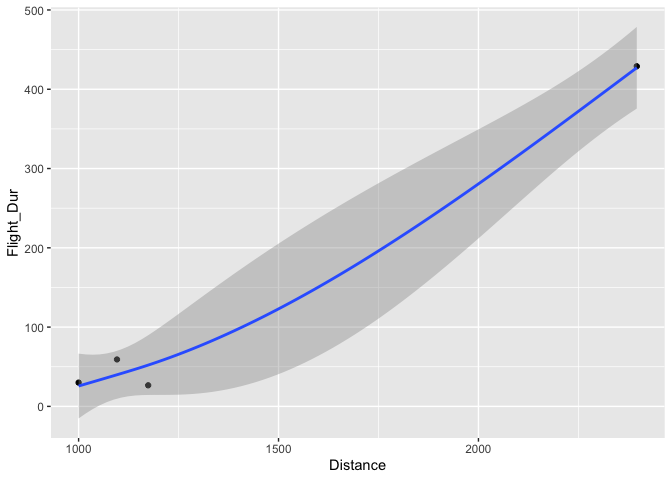
^{Created on 2022-09-13 by the reprex package (v1.0.0)}

However, I would be a bit careful to use a gam with so few observations.