How not to have overlayed plots in Python (to save as an image AND as a Latex file)?-CodePudding

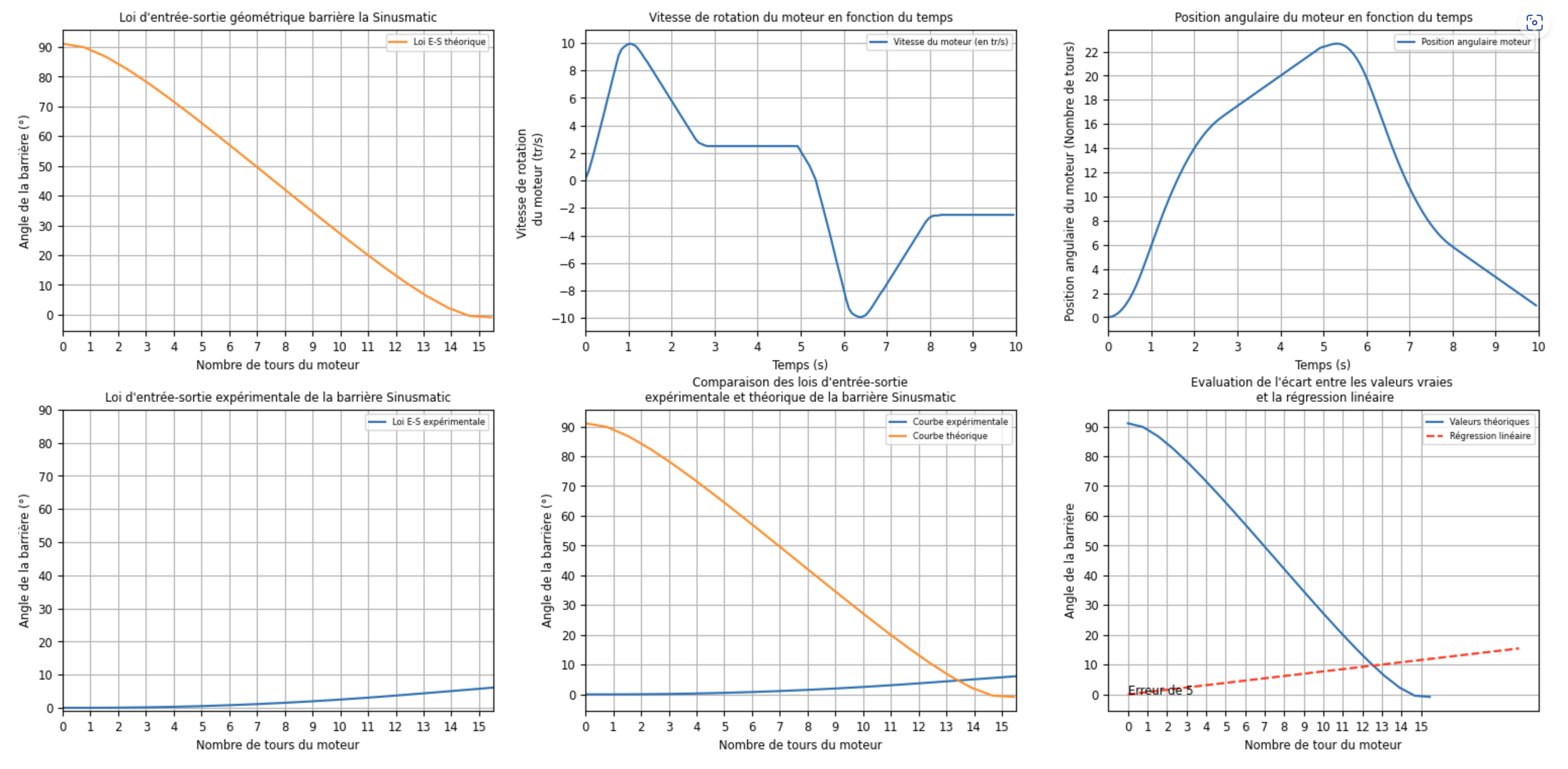
I'm currently dealing with different plots at once and I would like to be able to save it as an image OR to save it as a .tex file (Latex) to be able to import it on my Latex document but when I'm using the plt.savefig(...) or the tikzplotlib.save(...) (with the appropriate environment) the result is just something with overlayed subplots.

So I would like to be able to 'collect' the figure in the right way for everything to looks nice (no overlaying)

I already tried to add a tight_layout but it doesn't seem to change anything.

Here is what I've got and what I would like as well as the python code I'm running :

Python code

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import tikzplotlib
from matplotlib import rc

#The variables
angle_moteur_theorique = np.array([ 0.  ,  0.77190147,  1.54380295,  2.31570442,  3.0876059 , 3.85950737,  4.63140884,  5.40331032,  6.17521179,  6.94711327, 7.71901474,  8.49091621,  9.26281769, 10.03471916, 10.80662064, 11.57852211, 12.35042358, 13.12232506, 13.89422653, 14.66612801, 15.43802948])
angle_barriere_theorique = np.array([91.07866731, 89.85870606, 86.72892154, 82.55520246, 77.7604672, 72.57406548, 67.13171026, 61.52013482, 55.79906609, 50.0130552 , 44.1985095 , 38.38846038, 32.61646301, 26.92062793, 21.34884296, 15.96679822, 10.87188966,  6.21969357,  2.27915911, -0.44028002, -0.86128366])
Temps = np.array([0.  , 0.  , 0.07, 0.14, 0.21, 0.28, 0.35, 0.42, 0.49, 0.56, 0.63, 0.7 , 0.77, 0.84, 0.91, 0.98, 1.05, 1.16, 1.23, 1.3 , 1.37, 1.44, 1.51, 1.58, 1.65, 1.72, 1.79, 1.86, 1.93, 2.  , 2.07, 2.14, 2.21, 2.28, 2.35, 2.42, 2.49, 2.56, 2.63, 2.7 , 2.77, 2.84, 2.91, 2.98, 3.05, 3.12, 3.19, 3.26, 3.33, 3.4 , 3.47, 3.54, 3.61, 3.68, 3.75, 3.82, 3.89, 3.96, 4.03, 4.1 , 4.17, 4.24, 4.31, 4.37, 4.44, 4.51, 4.58, 4.65, 4.72, 4.79, 4.86, 4.93, 5.21, 5.28, 5.35, 5.42, 5.49, 5.56, 5.63, 5.7 , 5.77, 5.84, 5.91, 5.98, 6.05, 6.12, 6.19, 6.26, 6.33, 6.4 , 6.51, 6.58, 6.65, 6.72, 6.79, 6.86, 6.93, 7.  , 7.07, 7.14, 7.21, 7.28, 7.35, 7.42, 7.49, 7.56, 7.63, 7.7 , 7.77, 7.84, 7.91, 7.98, 8.05, 8.12, 8.19, 8.26, 8.33, 8.4 , 8.47, 8.54, 8.61, 8.68, 8.75, 8.82, 8.89, 8.96, 9.03, 9.1 , 9.17, 9.24, 9.31, 9.38, 9.45, 9.52, 9.59, 9.66, 9.73, 9.8 , 9.87, 9.94])
Vitesse_moteur_corrigee = np.array([ 0.  ,  0.15,  0.65,  1.4 ,  2.2 ,  3.05,  3.9 ,  4.75,  5.65, 6.5 ,  7.4 ,  8.25,  9.1 ,  9.55,  9.75,  9.9 ,  9.95,  9.8 , 9.55,  9.25,  8.9 ,  8.6 ,  8.25,  7.9 ,  7.55,  7.2 ,  6.85, 6.5 ,  6.15,  5.8 ,  5.45,  5.1 ,  4.75,  4.4 ,  4.05,  3.7 , 3.35,  3.  ,  2.75,  2.65,  2.55,  2.5 ,  2.5 ,  2.5 ,  2.5 , 2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 , 2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 , 2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 , 1.05,  0.55,  0.05, -0.8 , -1.6 , -2.45, -3.3 , -4.15, -5.05, -5.95, -6.8 , -7.65, -8.55, -9.3 , -9.65, -9.8 , -9.9 , -9.95, -9.8 , -9.55, -9.25, -8.9 , -8.55, -8.2 , -7.9 , -7.55, -7.2 , -6.85, -6.5 , -6.15, -5.8 , -5.45, -5.1 , -4.75, -4.4 , -4.05, -3.7 , -3.35, -3.  , -2.75, -2.6 , -2.55, -2.55, -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 ])
position_angulaire_moteur = np.array([ 0.   ,  0.   ,  0.046,  0.144,  0.298,  0.512,  0.785,  1.118, 1.514,  1.969,  2.487,  3.064,  3.701,  4.369,  5.052,  5.745, 6.442,  7.52 ,  8.188,  8.836,  9.459, 10.061, 10.638, 11.191, 11.72 , 12.224, 12.704, 13.159, 13.59 , 13.996, 14.378, 14.735, 15.067, 15.375, 15.659, 15.918, 16.152, 16.362, 16.554, 16.74 , 16.918, 17.093, 17.268, 17.443, 17.618, 17.793, 17.968, 18.143, 18.318, 18.493, 18.668, 18.843, 19.018, 19.193, 19.368, 19.543, 19.718, 19.893, 20.068, 20.243, 20.418, 20.593, 20.768, 20.918, 21.093, 21.268, 21.443, 21.618, 21.793, 21.968, 22.143, 22.318, 22.612, 22.65 , 22.653, 22.597, 22.485, 22.314, 22.083, 21.792, 21.439, 21.022, 20.546, 20.01 , 19.412, 18.761, 18.085, 17.399, 16.706, 16.009, 14.931, 14.262, 13.614, 12.991, 12.392, 11.818, 11.265, 10.736, 10.232,  9.753,  9.298,  8.867,  8.461,  8.079, 7.722,  7.39 ,  7.082,  6.798,  6.539,  6.304,  6.094,  5.901, 5.719,  5.541,  5.362,  5.187,  5.012,  4.837,  4.662,  4.487, 4.312,  4.137,  3.962,  3.787,  3.612,  3.437,  3.262,  3.087, 2.912,  2.737,  2.562,  2.387,  2.212,  2.037,  1.862,  1.687, 1.512,  1.337,  1.162,  0.987])
indice_premier_palier = 41
Positions = np.array([89.47, 89.35, 89.57, 89.47, 89.04, 88.41, 87.35, 85.86, 83.84,81.3 , 78.1 , 74.28, 69.62, 64.72, 59.65, 53.91, 48.61, 40.54,34.9 , 29.71, 24.29, 19.41, 15.07, 11.22,  7.72,  4.34,  1.26,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.74,3.7 ,  6.98, 10.92, 15.48, 20.68, 26.41, 32.04, 37.66, 43.29,51.57, 57.1 , 61.97, 66.75, 71.21, 75.56, 79.27, 82.9 , 85.86,88.3 , 90.09, 89.47, 88.61, 89.04, 89.78, 89.35, 89.47, 89.67,89.78, 89.67, 89.67, 89.78, 89.78, 89.78, 89.78, 89.78, 89.89,89.78, 89.78, 89.89, 89.89, 89.78, 89.78, 89.78, 89.78, 89.78,89.78, 89.78, 89.78, 89.78, 89.89, 89.78, 89.78, 89.78, 89.78,89.78, 89.89, 89.78, 89.78, 89.78])
Reg_lin = np.array([96.93466899, 91.67787419, 86.42107939, 81.16428459, 75.90748979,70.65069499, 65.39390019, 60.13710539, 54.88031058, 49.62351578,44.36672098, 39.10992618, 33.85313138, 28.59633658, 23.33954178,18.08274698, 12.82595218,  7.56915738,  2.31236258, -2.94443222,-8.20122702])
ERREUR = 5



def conclusion():
    fig, axs = plt.subplots(2,3)

    axs[0,0].plot(angle_moteur_theorique, angle_barriere_theorique, color='#ff7f0e', label='Loi E-S théorique')
    axs[0,0].set_xlabel('Nombre de tours du moteur', fontsize='small')
    axs[0,0].set_ylabel('Angle de la barrière (°)', fontsize='small')
    axs[0,0].set_yticks([10*i for i in range(0,10)])
    axs[0,0].set_xticks([i for i in range(0,16)])
    axs[0,0].grid(True)
    axs[0,0].set_title('Loi d\'entrée-sortie géométrique barrière la Sinusmatic', fontsize='small')
    axs[0,0].set_xlim(0,15.5)
    axs[0,0].tick_params(axis='both', which='major', labelsize='small')
    axs[0,0].tick_params(axis='both', which='minor', labelsize='small')
    axs[0,0].legend(loc='best', prop={'size':6})


    axs[0,1].plot(Temps, Vitesse_moteur_corrigee, label='Vitesse du moteur (en tr/s)')
    axs[0,1].set_xlabel('Temps (s)', fontsize='small')
    axs[0,1].set_ylabel('Vitesse de rotation \n du moteur (tr/s)', fontsize='small')
    axs[0,1].set_title('Vitesse de rotation du moteur en fonction du temps', fontsize='small')
    axs[0,1].set_xticks([i for i in range(0,11)])
    axs[0,1].set_yticks([i for i in range(-10,11,2)])
    axs[0,1].set_xlim(0,10)
    axs[0,1].grid()
    axs[0,1].tick_params(axis='both', which='major', labelsize='small')
    axs[0,1].tick_params(axis='both', which='minor', labelsize='small')
    axs[0,1].legend(loc='best', prop={'size':6})


    axs[0,2].plot(Temps, position_angulaire_moteur, label='Position angulaire moteur')
    axs[0,2].set_xlabel('Temps (s)', fontsize='small')
    axs[0,2].set_ylabel('Position angulaire du moteur (Nombre de tours)', fontsize='small')
    axs[0,2].set_title('Position angulaire du moteur en fonction du temps', fontsize='small')
    axs[0,2].set_xticks([i for i in range(0,11)])
    axs[0,2].set_yticks([i for i in range(0,23,2)])
    axs[0,2].set_xlim(0,10)
    axs[0,2].grid()
    axs[0,2].tick_params(axis='both', which='major', labelsize='small')
    axs[0,2].tick_params(axis='both', which='minor', labelsize='small')
    axs[0,2].legend(loc='best', prop={'size':6})


    axs[1,0].plot(position_angulaire_moteur[:indice_premier_palier], Position[:indice_premier_palier], label='Loi E-S expérimentale')
    axs[1,0].set_xlabel('Nombre de tours du moteur', fontsize='small')
    axs[1,0].set_ylabel('Angle de la barrière (°)', fontsize='small')
    axs[1,0].set_yticks([10*i for i in range(0,10)])
    axs[1,0].set_xticks([i for i in range(0,16)])
    axs[1,0].grid(True)
    axs[1,0].set_title('Loi d\'entrée-sortie expérimentale de la barrière Sinusmatic', fontsize='small')
    axs[1,0].set_xlim(0,15.5)
    axs[1,0].tick_params(axis='both', which='major', labelsize='small')
    axs[1,0].tick_params(axis='both', which='minor', labelsize='small')
    axs[1,0].legend(loc='best', prop={'size':6})


    axs[1,1].plot(position_angulaire_moteur[:indice_premier_palier], Position[:indice_premier_palier], label='Courbe expérimentale')
    axs[1,1].plot(angle_moteur_theorique, angle_barriere_theorique, label='Courbe théorique')
    axs[1,1].set_xlabel('Nombre de tours du moteur', fontsize='small')
    axs[1,1].set_ylabel('Angle de la barrière (°)', fontsize='small')
    axs[1,1].set_yticks([10*i for i in range(0,10)])
    axs[1,1].set_xticks([i for i in range(0,16)])
    axs[1,1].grid(True)
    axs[1,1].set_title('Comparaison des lois d\'entrée-sortie\nexpérimentale et théorique de la barrière Sinusmatic', fontsize='small')
    axs[1,1].set_xlim(0,15.5)
    axs[1,1].legend(loc='best', prop={'size':6})
    axs[1,1].tick_params(axis='both', which='major', labelsize='small')
    axs[1,1].tick_params(axis='both', which='minor', labelsize='small')


    axs[1,2].plot(angle_moteur_theorique, angle_barriere_theorique, color='#1f77b4', label = 'Valeurs théoriques')
    axs[1,2].plot(angle_moteur_theorique, reg_lin, 'r--', label = 'Régression linéaire')
    axs[1,2].set_title('Evaluation de l\'écart entre les valeurs vraies \n et la régression linéaire', fontsize='small')
    axs[1,2].set_xlabel('Nombre de tour du moteur', fontsize='small')
    axs[1,2].set_ylabel('Angle de la barrière', fontsize='small')
    axs[1,2].text(0,0,'Erreur de '   str(round(ERREUR,2)), fontsize='small')
    axs[1,2].legend(loc = 'best', prop={'size':6})
    axs[1,2].set_yticks([10*i for i in range(0,10)])
    axs[1,2].set_xticks([i for i in range(0,16)])
    axs[1,2].grid(True)
    axs[1,2].tick_params(axis='both', which='major', labelsize='small')
    axs[1,2].tick_params(axis='both', which='minor', labelsize='small')

The end of the function conclusion() depends on what I'm doing :

1. Saving the plots as an image : the end of the function is :

    fig.tight_layout(pad=0.1)
    plt.savefig('Bilan.png', dpi=1200, bbox_inches='tight')

2. Saving the plots as a tex file : the end of the function is :

    fig.tight_layout(pad=0.1)
    tikzplotlib.save('Bilan.tex')

The environment for the Latex file is this one, that should be run before executing the function :

matplotlib.use("pgf")
matplotlib.rcParams.update({
    "pgf.texsystem": "pdflatex",
    'font.family': 'serif',
    'text.usetex': True,
    'pgf.rcfonts': False,
})

To save the plots as a picture, this is the environment to use, that should be run before executing the function :

matplotlib.use("MacOSX")
matplotlib.rcParams.update({
    "pgf.texsystem": "pdflatex",
    'font.family': 'serif',
    'text.usetex': True,
    'pgf.rcfonts': False,
})

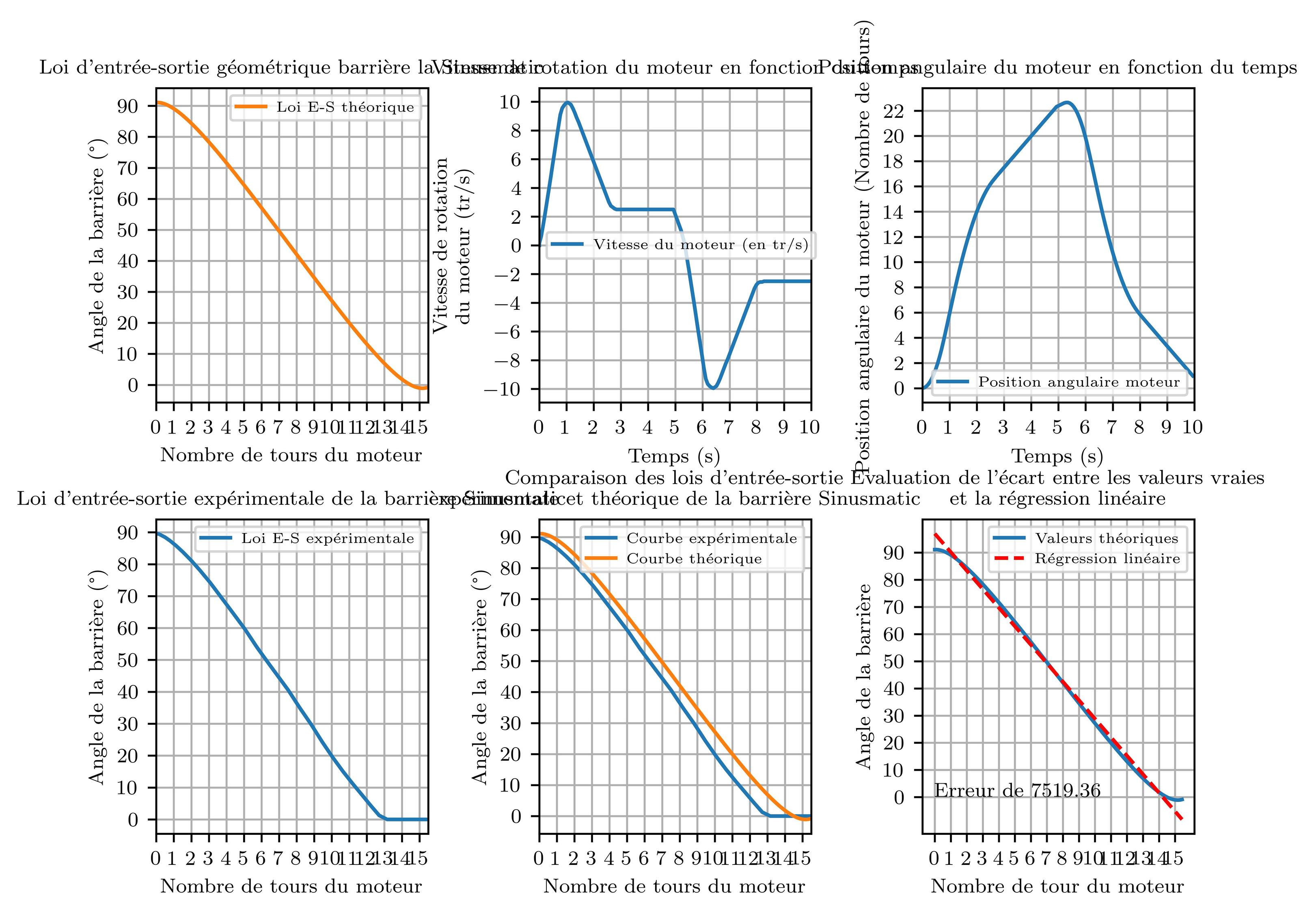
So, here is what I would like (the goal):

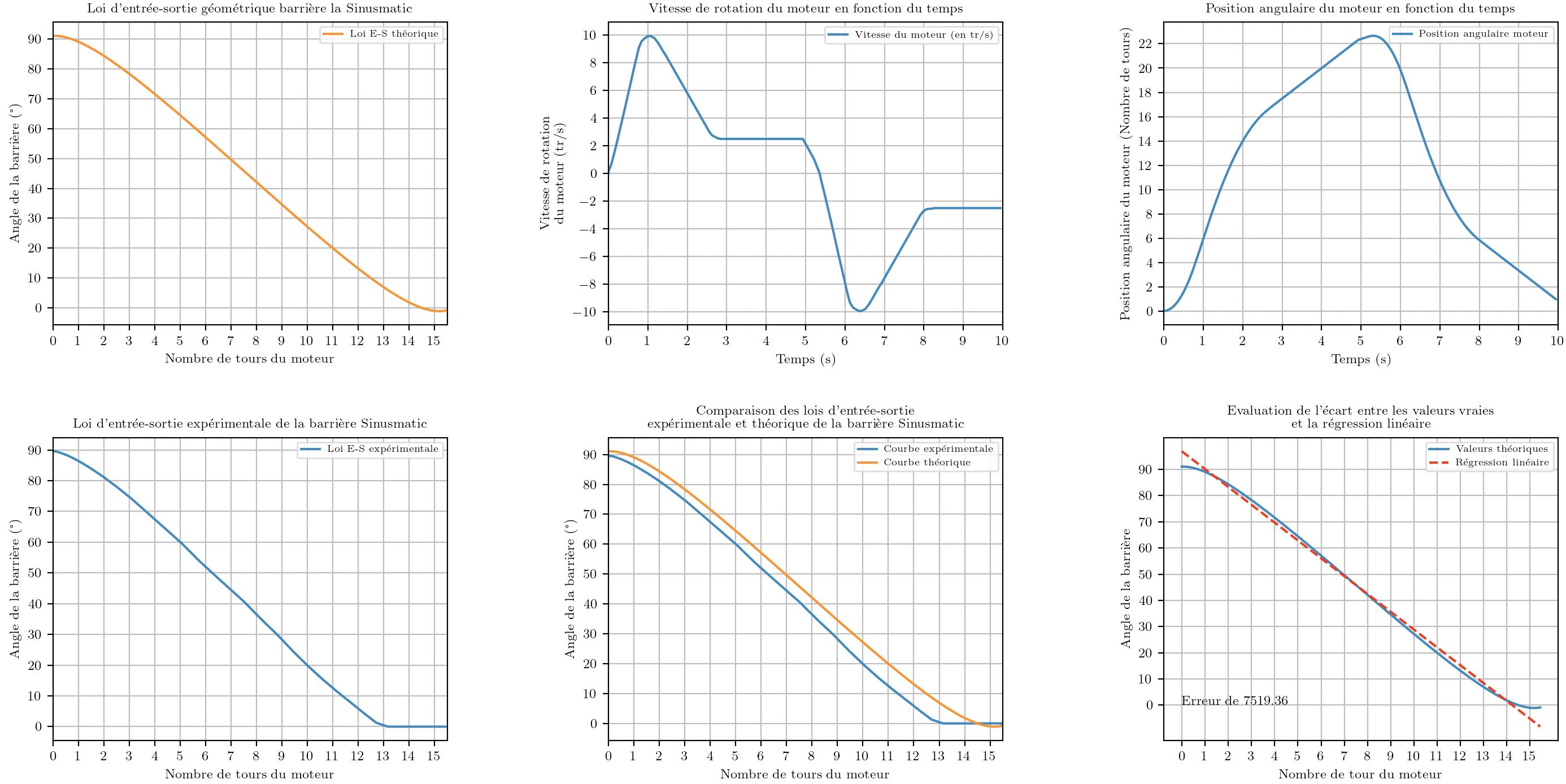
and this is what I currently have :

1. When saving as an image :

2. When saving as a tex file :

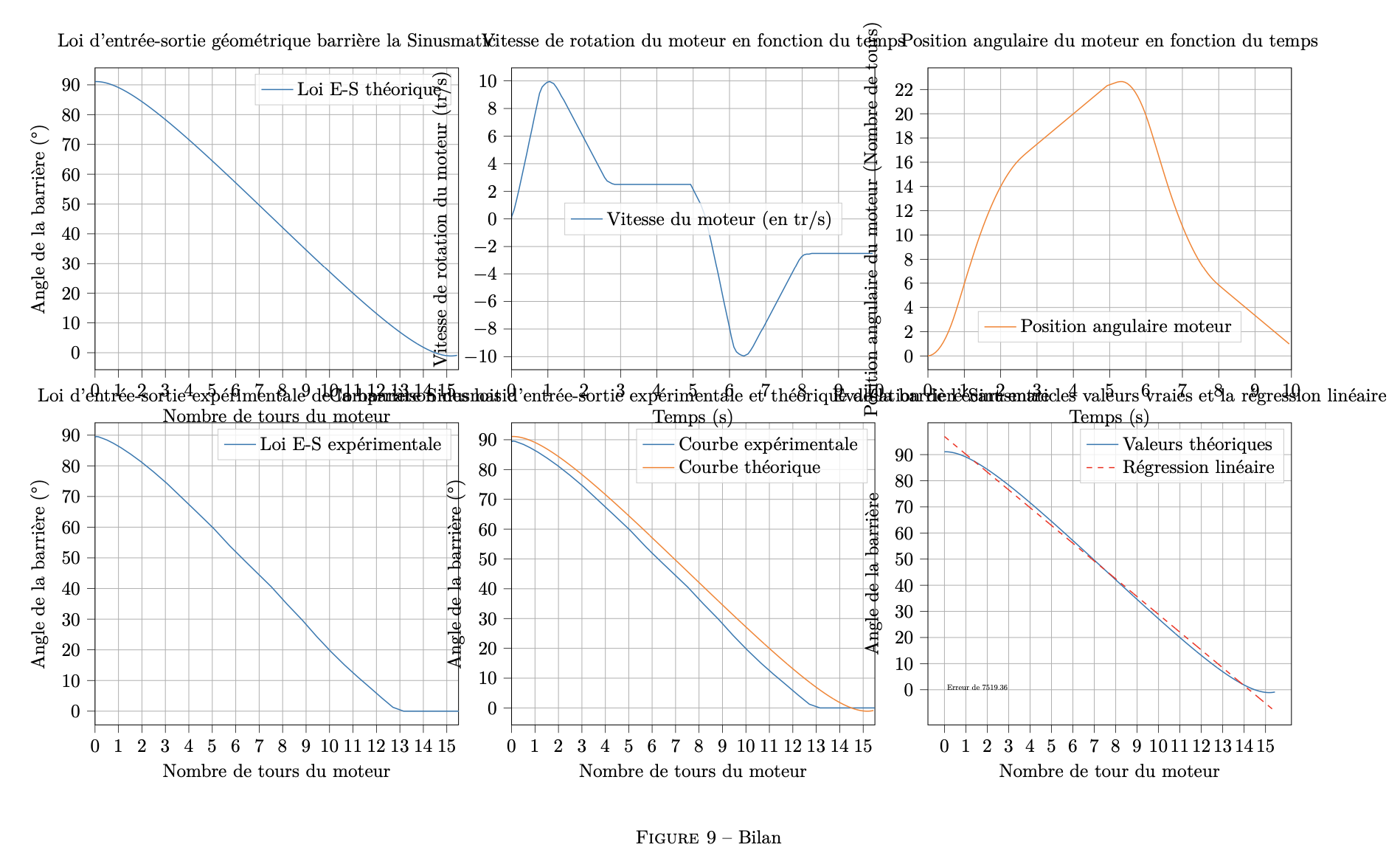
And here is the Latex code, if needed :

\documentclass[a4paper]{article}

\usepackage{lscape}

\begin{document}
    \begin{landscape}
        \begin{figure}[ht!]
            \begin{center}
                \input{Bilan.tex}
            \end{center} 
            \caption{Bilan} 
        \end{figure}
    \end{landscape}
\end{document}

CodePudding user response：

I was fiddling with your code a little and unless I am missing something a simple export to a pdf with fig.tight_layout(pad=3.5) and plt.savefig('example.pdf') seems to work all right (perhaps tight_layout should be a little larger). I haven't touched font size of your labels but everything else seems to look Okey.

This is what the code in jupyter prints out:

The code I altered exports the figure to a PDF and \includegraphics is what I use in LaTeX; note I wrap the figure inside sidewaysfigure environment in order to rotate it and utilise the whole available space. To me, this is rather a clear presentation apart from small fonts

The code for LaTeX

\documentclass{article}
\usepackage{rotating}
\usepackage{graphicx}
\usepackage{caption}

\captionsetup[figure]{skip=0pt,position=bottom}

\usepackage{kantlipsum}   % Required only for dummy text (\kant[X][Y])
\usepackage{showframe}    % Draws frame around the page in PDF
\renewcommand*{\ShowFrameLinethickness}{0.2pt}
\renewcommand*{\ShowFrameColor}{\color{blue}}


\begin{document}
\kant[1-3]

Reference to the figure~\ref{fig:six-figures}

\begin{sidewaysfigure}
  \includegraphics[width=\textheight]{example}
  \caption{The six figures.}\label{fig:six-figures}
\end{sidewaysfigure}

\end{document}

The code for jupyter notebook (Python)

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# import tikzplotlib
from matplotlib import rc

#The variables
angle_moteur_theorique = np.array([ 0.  ,  0.77190147,  1.54380295,  2.31570442,  3.0876059 , 3.85950737,  4.63140884,  5.40331032,  6.17521179,  6.94711327, 7.71901474,  8.49091621,  9.26281769, 10.03471916, 10.80662064, 11.57852211, 12.35042358, 13.12232506, 13.89422653, 14.66612801, 15.43802948])
angle_barriere_theorique = np.array([91.07866731, 89.85870606, 86.72892154, 82.55520246, 77.7604672, 72.57406548, 67.13171026, 61.52013482, 55.79906609, 50.0130552 , 44.1985095 , 38.38846038, 32.61646301, 26.92062793, 21.34884296, 15.96679822, 10.87188966,  6.21969357,  2.27915911, -0.44028002, -0.86128366])
Temps = np.array([0.  , 0.  , 0.07, 0.14, 0.21, 0.28, 0.35, 0.42, 0.49, 0.56, 0.63, 0.7 , 0.77, 0.84, 0.91, 0.98, 1.05, 1.16, 1.23, 1.3 , 1.37, 1.44, 1.51, 1.58, 1.65, 1.72, 1.79, 1.86, 1.93, 2.  , 2.07, 2.14, 2.21, 2.28, 2.35, 2.42, 2.49, 2.56, 2.63, 2.7 , 2.77, 2.84, 2.91, 2.98, 3.05, 3.12, 3.19, 3.26, 3.33, 3.4 , 3.47, 3.54, 3.61, 3.68, 3.75, 3.82, 3.89, 3.96, 4.03, 4.1 , 4.17, 4.24, 4.31, 4.37, 4.44, 4.51, 4.58, 4.65, 4.72, 4.79, 4.86, 4.93, 5.21, 5.28, 5.35, 5.42, 5.49, 5.56, 5.63, 5.7 , 5.77, 5.84, 5.91, 5.98, 6.05, 6.12, 6.19, 6.26, 6.33, 6.4 , 6.51, 6.58, 6.65, 6.72, 6.79, 6.86, 6.93, 7.  , 7.07, 7.14, 7.21, 7.28, 7.35, 7.42, 7.49, 7.56, 7.63, 7.7 , 7.77, 7.84, 7.91, 7.98, 8.05, 8.12, 8.19, 8.26, 8.33, 8.4 , 8.47, 8.54, 8.61, 8.68, 8.75, 8.82, 8.89, 8.96, 9.03, 9.1 , 9.17, 9.24, 9.31, 9.38, 9.45, 9.52, 9.59, 9.66, 9.73, 9.8 , 9.87, 9.94])
Vitesse_moteur_corrigee = np.array([ 0.  ,  0.15,  0.65,  1.4 ,  2.2 ,  3.05,  3.9 ,  4.75,  5.65, 6.5 ,  7.4 ,  8.25,  9.1 ,  9.55,  9.75,  9.9 ,  9.95,  9.8 , 9.55,  9.25,  8.9 ,  8.6 ,  8.25,  7.9 ,  7.55,  7.2 ,  6.85, 6.5 ,  6.15,  5.8 ,  5.45,  5.1 ,  4.75,  4.4 ,  4.05,  3.7 , 3.35,  3.  ,  2.75,  2.65,  2.55,  2.5 ,  2.5 ,  2.5 ,  2.5 , 2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 , 2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 , 2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 ,  2.5 , 1.05,  0.55,  0.05, -0.8 , -1.6 , -2.45, -3.3 , -4.15, -5.05, -5.95, -6.8 , -7.65, -8.55, -9.3 , -9.65, -9.8 , -9.9 , -9.95, -9.8 , -9.55, -9.25, -8.9 , -8.55, -8.2 , -7.9 , -7.55, -7.2 , -6.85, -6.5 , -6.15, -5.8 , -5.45, -5.1 , -4.75, -4.4 , -4.05, -3.7 , -3.35, -3.  , -2.75, -2.6 , -2.55, -2.55, -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 , -2.5 ])
position_angulaire_moteur = np.array([ 0.   ,  0.   ,  0.046,  0.144,  0.298,  0.512,  0.785,  1.118, 1.514,  1.969,  2.487,  3.064,  3.701,  4.369,  5.052,  5.745, 6.442,  7.52 ,  8.188,  8.836,  9.459, 10.061, 10.638, 11.191, 11.72 , 12.224, 12.704, 13.159, 13.59 , 13.996, 14.378, 14.735, 15.067, 15.375, 15.659, 15.918, 16.152, 16.362, 16.554, 16.74 , 16.918, 17.093, 17.268, 17.443, 17.618, 17.793, 17.968, 18.143, 18.318, 18.493, 18.668, 18.843, 19.018, 19.193, 19.368, 19.543, 19.718, 19.893, 20.068, 20.243, 20.418, 20.593, 20.768, 20.918, 21.093, 21.268, 21.443, 21.618, 21.793, 21.968, 22.143, 22.318, 22.612, 22.65 , 22.653, 22.597, 22.485, 22.314, 22.083, 21.792, 21.439, 21.022, 20.546, 20.01 , 19.412, 18.761, 18.085, 17.399, 16.706, 16.009, 14.931, 14.262, 13.614, 12.991, 12.392, 11.818, 11.265, 10.736, 10.232,  9.753,  9.298,  8.867,  8.461,  8.079, 7.722,  7.39 ,  7.082,  6.798,  6.539,  6.304,  6.094,  5.901, 5.719,  5.541,  5.362,  5.187,  5.012,  4.837,  4.662,  4.487, 4.312,  4.137,  3.962,  3.787,  3.612,  3.437,  3.262,  3.087, 2.912,  2.737,  2.562,  2.387,  2.212,  2.037,  1.862,  1.687, 1.512,  1.337,  1.162,  0.987])
indice_premier_palier = 41
Positions = np.array([89.47, 89.35, 89.57, 89.47, 89.04, 88.41, 87.35, 85.86, 83.84,81.3 , 78.1 , 74.28, 69.62, 64.72, 59.65, 53.91, 48.61, 40.54,34.9 , 29.71, 24.29, 19.41, 15.07, 11.22,  7.72,  4.34,  1.26,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.74,3.7 ,  6.98, 10.92, 15.48, 20.68, 26.41, 32.04, 37.66, 43.29,51.57, 57.1 , 61.97, 66.75, 71.21, 75.56, 79.27, 82.9 , 85.86,88.3 , 90.09, 89.47, 88.61, 89.04, 89.78, 89.35, 89.47, 89.67,89.78, 89.67, 89.67, 89.78, 89.78, 89.78, 89.78, 89.78, 89.89,89.78, 89.78, 89.89, 89.89, 89.78, 89.78, 89.78, 89.78, 89.78,89.78, 89.78, 89.78, 89.78, 89.89, 89.78, 89.78, 89.78, 89.78,89.78, 89.89, 89.78, 89.78, 89.78])
Reg_lin = np.array([96.93466899, 91.67787419, 86.42107939, 81.16428459, 75.90748979,70.65069499, 65.39390019, 60.13710539, 54.88031058, 49.62351578,44.36672098, 39.10992618, 33.85313138, 28.59633658, 23.33954178,18.08274698, 12.82595218,  7.56915738,  2.31236258, -2.94443222,-8.20122702])
ERREUR = 5

# matplotlib.use("pgf")
# matplotlib.rcParams.update({
#     "pgf.texsystem": "pdflatex",
#     'font.family': 'serif',
#     'text.usetex': True,
#     'pgf.rcfonts': False,
# })

def conclusion():
    fig, axs = plt.subplots(2,3, figsize=(16,8))
    fig.tight_layout(pad=3.5)

    axs[0,0].plot(angle_moteur_theorique, angle_barriere_theorique, color='#ff7f0e', label='Loi E-S théorique')
    axs[0,0].set_xlabel('Nombre de tours du moteur', fontsize='small')
    axs[0,0].set_ylabel('Angle de la barrière (°)', fontsize='small')
    axs[0,0].set_yticks([10*i for i in range(0,10)])
    axs[0,0].set_xticks([i for i in range(0,16)])
    axs[0,0].grid(True)
    axs[0,0].set_title('Loi d\'entrée-sortie géométrique barrière la Sinusmatic', fontsize='small')
    axs[0,0].set_xlim(0,15.5)
    axs[0,0].tick_params(axis='both', which='major', labelsize='small')
    axs[0,0].tick_params(axis='both', which='minor', labelsize='small')
    axs[0,0].legend(loc='best', prop={'size':6})

    axs[0,1].plot(Temps, Vitesse_moteur_corrigee, label='Vitesse du moteur (en tr/s)')
    axs[0,1].set_xlabel('Temps (s)', fontsize='small')
    axs[0,1].set_ylabel('Vitesse de rotation \n du moteur (tr/s)', fontsize='small')
    axs[0,1].set_title('Vitesse de rotation du moteur en fonction du temps', fontsize='small')
    axs[0,1].set_xticks([i for i in range(0,11)])
    axs[0,1].set_yticks([i for i in range(-10,11,2)])
    axs[0,1].set_xlim(0,10)
    axs[0,1].grid()
    axs[0,1].tick_params(axis='both', which='major', labelsize='small')
    axs[0,1].tick_params(axis='both', which='minor', labelsize='small')
    axs[0,1].legend(loc='best', prop={'size':6})

    axs[0,2].plot(Temps, position_angulaire_moteur, label='Position angulaire moteur')
    axs[0,2].set_xlabel('Temps (s)', fontsize='small')
    axs[0,2].set_ylabel('Position angulaire du moteur (Nombre de tours)', fontsize='small')
    axs[0,2].set_title('Position angulaire du moteur en fonction du temps', fontsize='small')
    axs[0,2].set_xticks([i for i in range(0,11)])
    axs[0,2].set_yticks([i for i in range(0,23,2)])
    axs[0,2].set_xlim(0,10)
    axs[0,2].grid()
    axs[0,2].tick_params(axis='both', which='major', labelsize='small')
    axs[0,2].tick_params(axis='both', which='minor', labelsize='small')
    axs[0,2].legend(loc='best', prop={'size':6})

    axs[1,0].plot(position_angulaire_moteur[:indice_premier_palier], label='Loi E-S expérimentale')   #Position[:indice_premier_palier], 
    axs[1,0].set_xlabel('Nombre de tours du moteur', fontsize='small')
    axs[1,0].set_ylabel('Angle de la barrière (°)', fontsize='small')
    axs[1,0].set_yticks([10*i for i in range(0,10)])
    axs[1,0].set_xticks([i for i in range(0,16)])
    axs[1,0].grid(True)
    axs[1,0].set_title('Loi d\'entrée-sortie expérimentale de la barrière Sinusmatic', fontsize='small')
    axs[1,0].set_xlim(0,15.5)
    axs[1,0].tick_params(axis='both', which='major', labelsize='small')
    axs[1,0].tick_params(axis='both', which='minor', labelsize='small')
    axs[1,0].legend(loc='best', prop={'size':6})

    axs[1,1].plot(position_angulaire_moteur[:indice_premier_palier], label='Courbe expérimentale') # Position[:indice_premier_palier], 
    axs[1,1].plot(angle_moteur_theorique, angle_barriere_theorique, label='Courbe théorique')
    axs[1,1].set_xlabel('Nombre de tours du moteur', fontsize='small')
    axs[1,1].set_ylabel('Angle de la barrière (°)', fontsize='small')
    axs[1,1].set_yticks([10*i for i in range(0,10)])
    axs[1,1].set_xticks([i for i in range(0,16)])
    axs[1,1].grid(True)
    axs[1,1].set_title('Comparaison des lois d\'entrée-sortie\nexpérimentale et théorique de la barrière Sinusmatic', fontsize='small')
    axs[1,1].set_xlim(0,15.5)
    axs[1,1].legend(loc='best', prop={'size':6})
    axs[1,1].tick_params(axis='both', which='major', labelsize='small')
    axs[1,1].tick_params(axis='both', which='minor', labelsize='small')

    axs[1,2].plot(angle_moteur_theorique, angle_barriere_theorique, color='#1f77b4', label = 'Valeurs théoriques')
    axs[1,2].plot(angle_moteur_theorique, 'r--', label = 'Régression linéaire')   # reg_lin, 
    axs[1,2].set_title('Evaluation de l\'écart entre les valeurs vraies \n et la régression linéaire', fontsize='small')
    axs[1,2].set_xlabel('Nombre de tour du moteur', fontsize='small')
    axs[1,2].set_ylabel('Angle de la barrière', fontsize='small')
    axs[1,2].text(0,0,'Erreur de '   str(round(ERREUR,2)), fontsize='small')
    axs[1,2].legend(loc = 'best', prop={'size':6})
    axs[1,2].set_yticks([10*i for i in range(0,10)])
    axs[1,2].set_xticks([i for i in range(0,16)])
    axs[1,2].grid(True)
    axs[1,2].tick_params(axis='both', which='major', labelsize='small')
    axs[1,2].tick_params(axis='both', which='minor', labelsize='small')
    
    plt.savefig('example.pdf')

# New cell
conclusion()