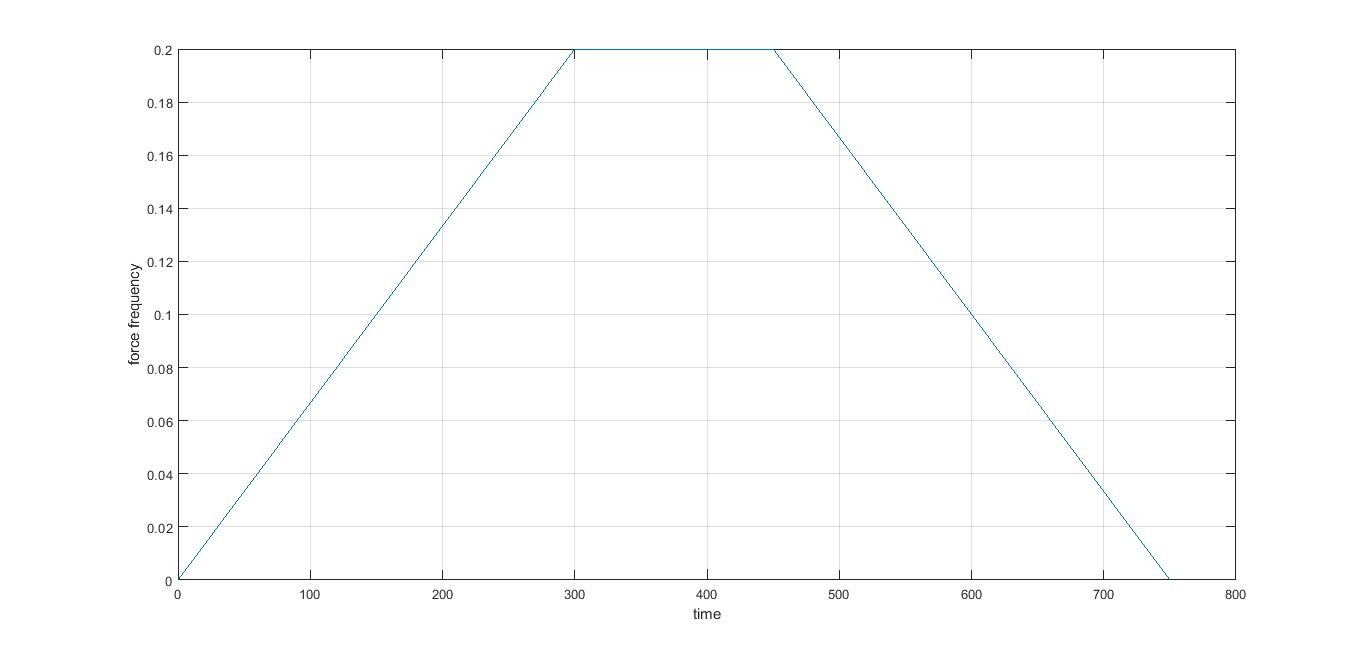
I have a machine in stationary mode. When it begins to run, its frequency changes linearly (from 0 to fully operational frequency), then becomes constant and finally begins to decrease linearly (from fully operational frequency to 0).

I wrote the following code for this:

te = 300;     % seconds - time to get fully operative 
              % (to arrive from 0 to fully operational frequency) 
              % and to stop (from fully operational to 0)
me = 10;      % eccentric mass
e = 0.5;      % eccentricity of the eccentric mass
omega=0.2;    % fully operational force frequency

%   i need three time vectors 
tt0=[0:0.1:te];                 %   uphill frequency part (from 0 to fully operational frequency)
tt1=[te 0.1:0.1:1.5*te];        %   permanent fully operational frequency part 
tt2=[1.5*te 0.1:0.1:2.5*te];    %   downward frequency part (from fully operational frequency to 0)

tt_1=[tt0,tt1,tt2];             %   whole time vector

n7=numel(tt_1);
n5=numel(tt0);
n6=numel(tt1);
n8=numel(tt2);

%   create a 3 force frequency vectors 
delta_omega1=omega/(n5-1);
delta_omega2=omega/(n8-1);
omega000=[0:delta_omega1:omega];    %   from 0 to fully operational frequency
omega001=omega*ones(1,n6);          %   permanent fully operational frequency part
omega002=[omega:-delta_omega2:0];   %   from fully operational frequency to 0

omega00=[omega000,omega001,omega002];   %   whole force frequency vector

p00=zeros(n7,1);
p_0010=zeros(n5,1);
p_0011=zeros(n6,1);
p_0012=zeros(n8,1);
p_001=zeros(n7,1);

%   force amplitude calculation
for j=1:n7
    p00(j,1) = (me*e*omega00(j)^2);
end
        
   
%   then i create 3 sin force vectors (for 3 different force frequency laws)
 for j=1:n5
    p_0010(j,1) = p00(j,1)*sin(omega/(2*te)*(tt0(j))^2);
end

for j=1:n6
    p_0011(j,1) = p00(j n5,1)*sin(omega*te omega*(tt1(j)-te));
end
    
for j=1:n8
    t2=tt2(1);
    p_0012(j,1) = p00(j n6 n5,1)*sin((-1/2*omega*te omega*tt2(j)-...
        1/2*omega/te*((t2-te)^2 (tt2(j)-t2)^2)));
end

p_001=[p_0010;p_0011;p_0012];   %   whole force vector


figure (1)
plot (tt_1,omega00)
xlabel('time')
ylabel('force frequency')
grid on;
hold on


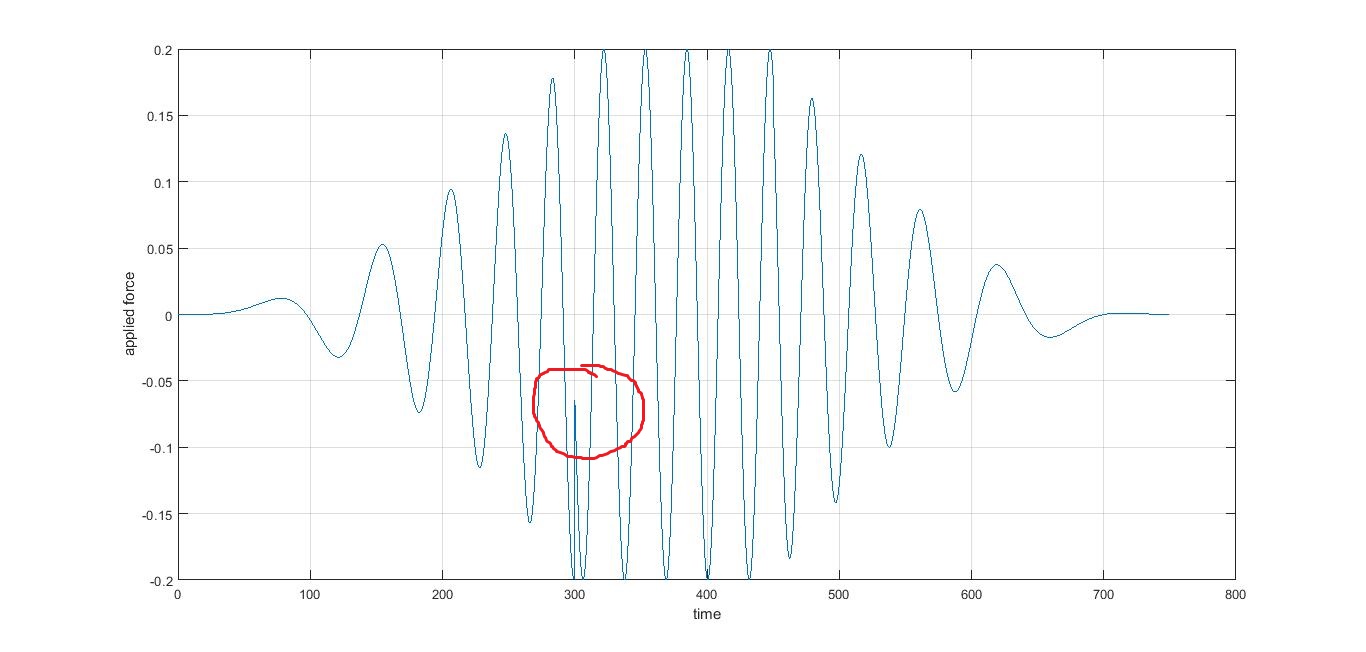
figure (2)
plot (tt_1,p_001)
xlabel('time')
ylabel('applied force')
grid on;
hold on

Which results in

This is correct.

But force diagram:

is incorrect.

How can I solve this problem? I don't need any discontinuity on the force diagram (because it produce a strange behavior of my system, like "parasite resonance" in this singular point).

CodePudding user response：

Your expression for the force is wrong. For unbalance force, its expression is me*omega^2*sin(omega*t) only if rotational speed omega is constant. If rotational speed is not constant (as is the case where it is linearly increasing or decreasing), its full expression is

For a rotary machine, you should have unbalance forces on the horizontal and vertical direction (second and third terms on the force vector above). δ is the phase angle, ϕ_dot is the rotational speed and ϕ_ddot is rotational acceleration. Notice that for linearly increasing or decreasing rotational speed, ϕ_ddot = α = constant, so your force expression should contain a term

α*cos(phi)

for constant acceleration, the angular position is just as you defined. Just define properly the initial angular position phi_0 for each time interval (they are not zero, they are the last position for the previous time interval).