Modify the algorithm to overcome the problem with the minimax for the game-CodePudding

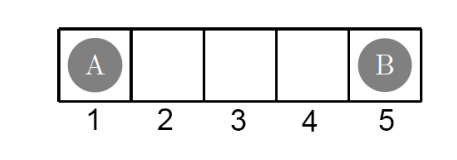
Players move in turns. A player moves first. Any player can move to an unoccupied adjacent square, or can teleport from one end of the board to the other end, given that the other end is not occupied. For example, if A is at second node, and B is at node 5 can go to both 4 and 1. If B wins (occupies 1 cell), game is valued as -1, If A wins (occupies 5 cell), game is valued as 1.

However, there is a problem of loops in this problem, how to modify the algorithm or maybe the heuristic to avoid the problem with this game?

The image of the game:

CodePudding user response：

Given the number of states is so small, it's easy just to brute-force this -- set won/loss states to 1 or -1, then repeatedly set any state to 1 if there's a move to a 1 state to 1 or -1 if all moves are to -1 states. Once there's no more changes, you have a solution and any undecided state is a draw by repetition.

Here's a program that does this. You can be a bit cleverer and exploit the symmetry between A and B to both reduce the number of states (and make the code a bit shorter), but this is the straightforward code:

def all_states():
    for p in range(2):
        for i in range(5):
            for j in range(5):
                if i == j: continue
                if i == 4 and j == 0: continue # impossible
                yield (p, i, j)

states = list(all_states())

def moves(s):
    p, i, j = s
    if p == 1:
        for p2, i2, j2 in moves((0, 4-j, 4-i)):
            yield 0, 4-j2, 4-i2
    else:
        for i2 in ((i-1)%5, (i 1)%5):
            if i2 != j:
                yield 1-p, i2, j

SCORE = {s: 1 if s[1] == 4 else -1 if s[2] == 0 else 0 for s in states}

change = True
while change:
    change = False
    for s in states:
        if SCORE[s] != 0: continue
        scores = [SCORE[s2] for s2 in moves(s)]
        if s[0] == 0 and 1 in scores:
            SCORE[s] = 1
            change = True
        elif s[0] == 0 and max(scores) == -1:
            SCORE[s] = -1
            change = True
        elif s[0] == 1 and -1 in scores:
            SCORE[s] = -1
            change = True
        elif s[0] == 1 and min(scores) == 1:
            SCORE[s] = 1
            change = True

def board(i, j):
    return ' '.join('A' if n==i else 'B' if n==j else 'x' for n in range(5))

for (p, i, j), sc in SCORE.items():
    print('AB'[p], 'to move: ', board(i, j), ' --', ['B wins', 'draw', 'A wins'][sc 1])

Output:

A to move:  A B x x x  -- A wins
A to move:  A x B x x  -- A wins
A to move:  A x x B x  -- A wins
A to move:  A x x x B  -- B wins
A to move:  B A x x x  -- B wins
A to move:  x A B x x  -- A wins
A to move:  x A x B x  -- B wins
A to move:  x A x x B  -- A wins
A to move:  B x A x x  -- B wins
A to move:  x B A x x  -- B wins
A to move:  x x A B x  -- A wins
A to move:  x x A x B  -- B wins
A to move:  B x x A x  -- B wins
A to move:  x B x A x  -- A wins
A to move:  x x B A x  -- A wins
A to move:  x x x A B  -- B wins
A to move:  x B x x A  -- A wins
A to move:  x x B x A  -- A wins
A to move:  x x x B A  -- A wins
B to move:  A B x x x  -- A wins
B to move:  A x B x x  -- A wins
B to move:  A x x B x  -- B wins
B to move:  A x x x B  -- A wins
B to move:  B A x x x  -- B wins
B to move:  x A B x x  -- B wins
B to move:  x A x B x  -- A wins
B to move:  x A x x B  -- B wins
B to move:  B x A x x  -- B wins
B to move:  x B A x x  -- B wins
B to move:  x x A B x  -- B wins
B to move:  x x A x B  -- B wins
B to move:  B x x A x  -- B wins
B to move:  x B x A x  -- B wins
B to move:  x x B A x  -- A wins
B to move:  x x x A B  -- B wins
B to move:  x B x x A  -- A wins
B to move:  x x B x A  -- A wins
B to move:  x x x B A  -- A wins

CodePudding user response：

We can make the following observations:

There are at most two valid moves at each turn.
If the players start such that A is at the left of B, then the one who can make the teleporting move first wins the game. So the best move for them is to walk towards their teleporting square. If they are already there, they should teleport, or if that is not possible, perform the only remaining move (in which case the other player can win on their next move).
If the players start such that A is at the right of B, the one who reaches their winning square first wins the game. So the best move for them is to walk towards their target square.

In other words, the player's best "strategy" is:

Don't play the (non-teleporting) move towards the opponent unless that is the only possible move.

So there is no reason to do minimax, not even a search. The best move can be known immediately from the current game state.