Find rotation needed to transform one point on sphere to another-CodePudding

I'm trying to make a basic sphere animation.

So far, I have some points lying on a sphere, which can be rotated around its origin by using the rotation matrices found on Wikipedia:

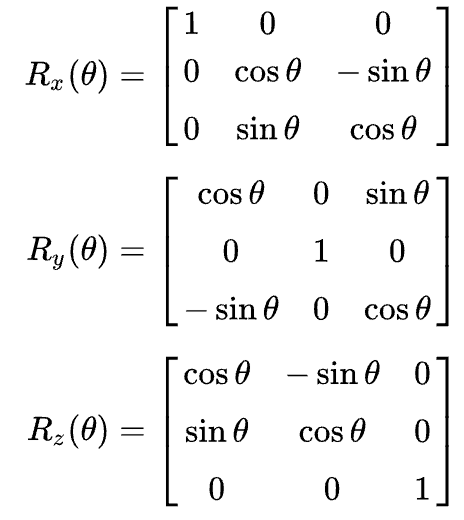
Rotation matrices

I now want to rotate the sphere so that a specific point is at the front (at [0, 0, 1]). I think that I might have to find the angle between the two vectors in each plane and rotate by this amount, but I'm not sure if this is correct, or how it can be achieved.

So, how would I find the angles required to do this?

CodePudding user response：

In spherical coordinates, your point is at (sin θ cos φ, sin θ sin φ, cos θ) where θ = arccos(z) and φ = atan2(y, x).
Beware of conventions: here, θ is the polar angle or inclination and φ is the azimuthal angle or azimuth.

Since you want to move your point to (0, 0, 1), you can first set φ to zero with a rotation around the z axis, and then set θ to zero with a rotation around the y axis.

The first rotation is Rz(-φ):

 cos φ   sin φ   0
-sin φ   cos φ   0
     0       0   1

The second rotation is Ry(-θ):

cos θ   0   -sin θ
    0   1        0
sin θ   0    cos θ

The composition is Ry(-θ) * Rz(-φ):

cos θ cos φ   cos θ sin φ   -sin θ
     -sin φ         cos φ        0
sin θ cos φ   sin θ sin φ    cos θ

Note that the last row is (x, y, z), which confirms that this point will move to (0, 0, 1).

Another way to construct a rotation matrix that takes (x, y, z) to (0, 0, 1), is to construct the inverse (that takes (0, 0, 1) to (x, y, z)) and then transpose it. You need three basis vectors that are perpendicular to each other, one for each column of the matrix. However, since we will transpose the result at the end, we can just consider these vectors to be the rows of the final matrix.

The first vector is V3 = (x, y, z), and this goes into the third row (since we want to move it to the z unit vector). The two other vectors can be computed using the cross-product with some other arbitrary vector. Many games and 3D engines use a "look-at" function that takes an "up" vector because the world usually has a sense of up and down.

Let's take UP = (0, 1, 0) as our "up" vector. You can compute V1 = norm(cross(UP, V3)) and V2 = cross(V3, V1). Depending on the order of arguments, you can flip the sphere (you can also multiply one of the vectors by -1). We don't need to normalize V2 since V1 and `V3 are both already unit vectors.

So the vectors are:

V3 = (x, y, z)
V1 = norm(cross(UP, V3)) = (z/sqrt(xx zz), 0, -x/sqrt(xx zz))
V2 = cross(V3, V1) = (-xy/sqrt(xx zz), sqrt(xx zz), -yz/sqrt(xx zz))

And the final rotation matrix, with S = sqrt(xx zz), is:

  z/S  0   -x/S
-xy/S  S  -yz/S
    x  y      z

Note that it's different from the one we obtained from Ry(-θ) * Rz(-φ). There are an infinite number of rotation matrices that move a point to another point, because rotations have three degrees of freedom and moving on a surface only has two if you don't consider the final orientation. You can get other results by changing the "up" vector.