scale_y_log10() affects p values in ggscatter-CodePudding

I am doing correlation graphs between two continous variables using ggscatter in ggstatsplot package. I am using the kendall rank coefficient with p-values automatically added to the graph. I want to use scale_y_log10() since there is a large spread on one of the measurements. However adding scale_y_log10() to the code affects the p-value.

Sampledata:

sampledata <- structure(list(ID = c(1, 2, 3, 4, 5), Measure1 = c(10, 10, 50, 0, 100), Measure2 = c(5, 3, 40, 30, 20), timepoint = c(1, 1,1, 1, 1), time = structure(c(18628, 19205, 19236, 19205, 19205), class = "Date"), event = c(1, 1, NA, NA, NA), eventdate = structure(c(18779,19024, NA, NA, NA), class = "Date")), row.names = c(NA, -5L), class = "data.frame")

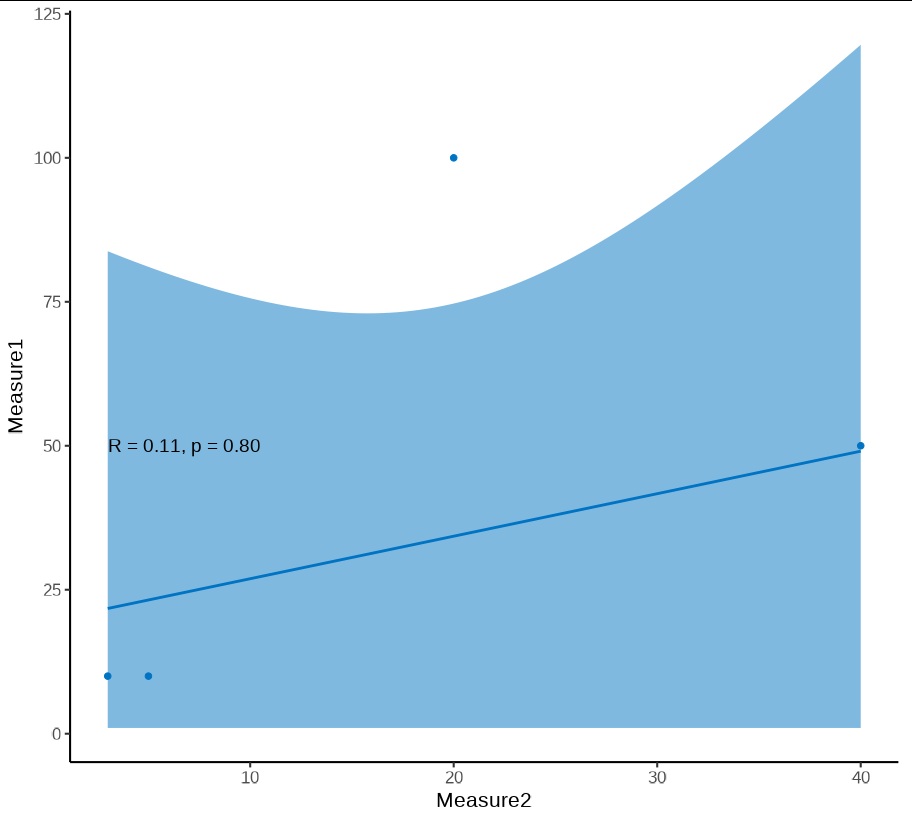
Graph without scale_y_log10()

ggscatter(data = sampledata, x = "Measure2", y = "Measure1",
      add = "reg.line", conf.int = TRUE, 
      cor.coef = TRUE, cor.method = "kendall",
      xlab = "measure2", ylab = "measure1", color="#0073C2FF" )

As you can see, R=0.11, P=0.8

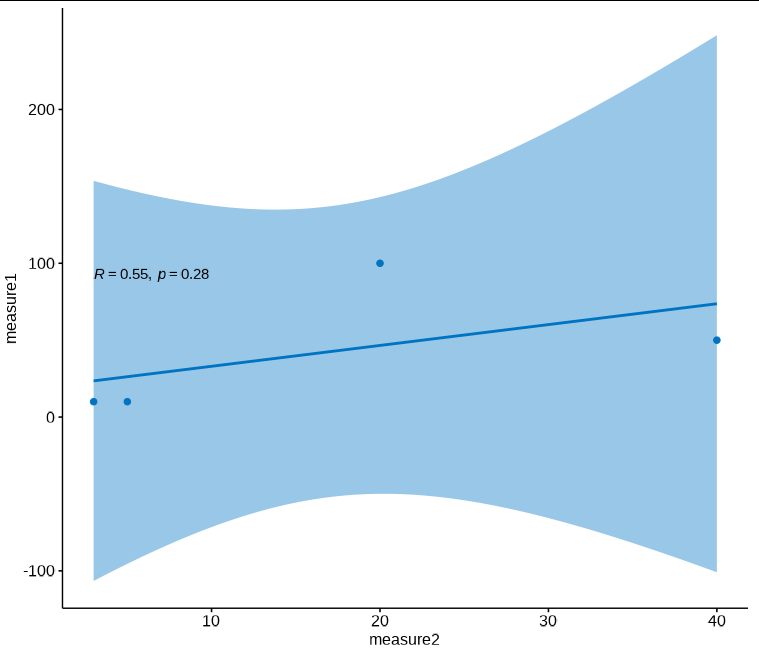
When adding scale_y_log10()

ggscatter(data = sampledata, x = "Measure2", y = "Measure1",
      add = "reg.line", conf.int = TRUE, 
      cor.coef = TRUE, cor.method = "kendall",
      xlab = "measure2", ylab = "measure1", color="#0073C2FF" )   scale_y_log10()

R=0.55 and P=0.28.

This is just some sample data and not my actual data.

Can anyone help me figure this out?

CodePudding user response：

The reason why your p value changes is that one of your y values (in variable Measure2 is 0. When you perform a log transform, this 0 value becomes minus infinity. It cannot be shown on the plot and is therefore removed from the plotting data. If you run ggscatter without this data point, you will see you get the same values as you do with a log transform:

ggscatter(data = subset(sampledata, Measure1 > 0),
          x = "Measure2", y = "Measure1",
          add = "reg.line", conf.int = TRUE,
          cor.coef = TRUE, cor.method = "kendall",
          xlab = "measure2", ylab = "measure1", color="#0073C2FF" )

You can also see that the y values of the confidence interval extend below 0, so the confidence interval in your log-transformed plot is not the same as the confidence interval in your non-transformed plot - the geom_smooth layer is basically doing its linear regression on log-transformed data, which probably isn't what you intended.

As with many ggplot extensions that make creating simple plots easier, one finds that if you want to do something unusual (like excluding 0 or negative values when adding a log scale), one cannot do it within that framework, and you therefore need to go back to vanilla ggplot to achieve what you want.

For example, you can create the points, line and ribbon, but excluding 0 or negative values like this:

mod <- lm(Measure1 ~ Measure2, data = sampledata)

xvals <- seq(3, 40, length.out = 100)
xvals <- c(xvals, rev(xvals))
preds <- predict(mod, newdata = data.frame(Measure2 = xvals), se.fit = TRUE)
lower <- preds$fit - 1.96 * preds$se.fit
upper <- preds$fit   1.96 * preds$se.fit
lower[lower < 1] <- 1

pred_df <- data.frame(Measure2 = xvals,
                      Measure1 = preds$fit)

polygon <- data.frame(Measure2 = xvals, 
                      Measure1 = c(lower[1:100], upper[101:200]))

ct <- cor.test(sampledata$Measure2, sampledata$Measure1, method = "kendall")

Now we can safely plot the data and style it to look like ggscatter:

p <- ggplot(subset(sampledata, Measure1 > 0),
       aes(Measure2, Measure1))  
  geom_polygon(data = polygon, fill = "#0073c2", alpha = 0.5)  
  geom_point(color = "#0073c2", size = 2)  
  geom_line(data = pred_df, color = "#0073c2", size = 1)  
  annotate("text", hjust = 0, x = min(sampledata$Measure2), y = 50, size = 5,
           label = paste0("R = ", sprintf("%1.2f", ct$estimate), ", p = ",
                          sprintf("%1.2f", ct$p.value)))  
  theme_classic(base_size = 16)

p

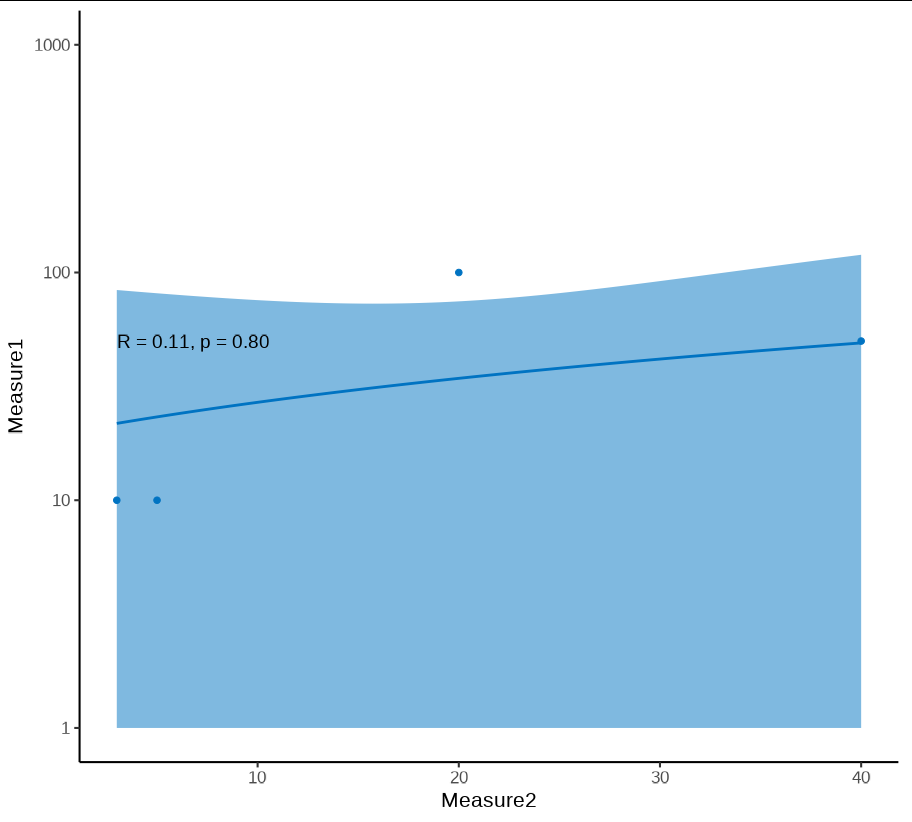
Except now we can safely log transform the output:

p   scale_y_log10(limits = c(1, 1000))