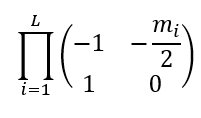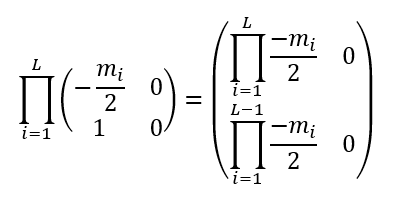Avoid overflow in random matrix multiplication in python-CodePudding

I have to multiply many (about 700) matrices with a random element (in the following, I'm using a box distribution) in python:

#define parameters
μ=2.
σ=2.
L=700

#define random matrix
T=[None]*L


product=np.array([[1,0],[0,1]])
for i in range(L):
    m=np.random.uniform(μ-σ*3**(1/2), μ σ*3**(1/2)) #box distribution
    T[i]=np.array([[-1,-m/2],[1,0]])
    product=product.dot(T[i])  #multiplying matrices

Det=abs(np.linalg.det(product))
print(Det)

For this choice of μ and σ, I obtain quantities of the order of e^30 , but this quantity should converge to 0. How do I know? Because analytically it can be demonstrated to be equivalent to:

Y=[None]*L
product1=np.array([[1,0],[0,1]])
for i in range(L):
    m=np.random.uniform(μ-σ*(3**(1/2)), μ σ*(3**(1/2))) #box distribution
    Y[i]=np.array([[-m/2,0],[1,0]])
    product1=product1.dot(Y[i])
    
l,v=np.linalg.eig(product1)

print(abs(l[1]))

which indeed gives e^-60. I think there is an overflow issue here. How can I fix it?

EDIT:

The two printed quantities are expected to be equivalent because the first one is the abs of the determinant of:

which is, according to the Binet theorem (the determinant of a product is the product of determinants):

The second code prints the abs of the greatest eigenvalue of:

It is easy to see that one eigenvalue is 0, the other equals .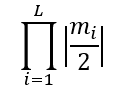

CodePudding user response：

It is generally a hard problem. There are a few nice articles about floating point arightmetics and precision. Here is a famous one

One of the general tricks - use a scale variable. Like this:

import numpy as np
#define parameters
μ=2.
σ=2.
L=700

#define random matrix
T=[None]*L

scale = 1
product=np.array([[1,0],[0,1]])
for i in range(L):
    m=np.random.uniform(μ-σ*3**(1/2), μ σ*3**(1/2)) #box distribution
    T[i]=np.array([[-1,-m/2],[1,0]])
    product=np.matmul(product, T[i])  #multiplying matrices
    scale *= abs(product[0][0])
    product /= abs(product[0][0])

Det=abs(np.linalg.det(product*scale))
print(Det)

It makes things a little better but unfortunately doesn't help.

In this particular case what you can do is multiply the determinants instead of matrices. Like this:

import numpy as np
#define parameters
μ=2.
σ=2.
L=700

#define random matrix
T=[None]*L

scale = 1
product=1
for i in range(L):
    m=np.random.uniform(μ-σ*3**(1/2), μ σ*3**(1/2)) #box distribution
    T[i]=np.array([[-1,-m/2],[1,0]])
    product *= np.linalg.det(T[i])  #multiplying matrices determinants
    
Det=abs(product)
print(Det)

The output:

1.1081329233309736e-61

So this cures the problem.