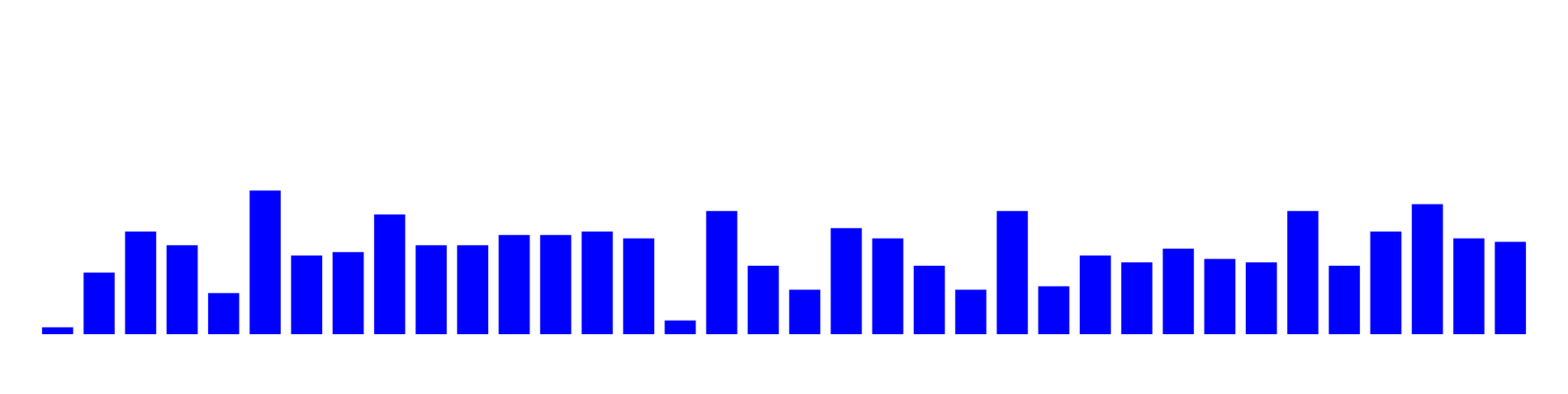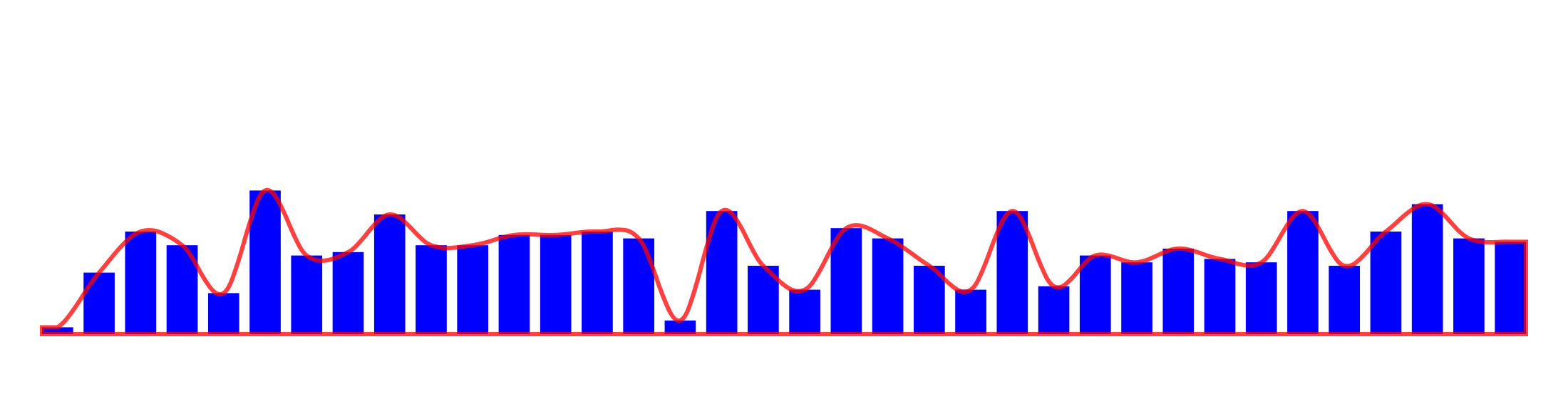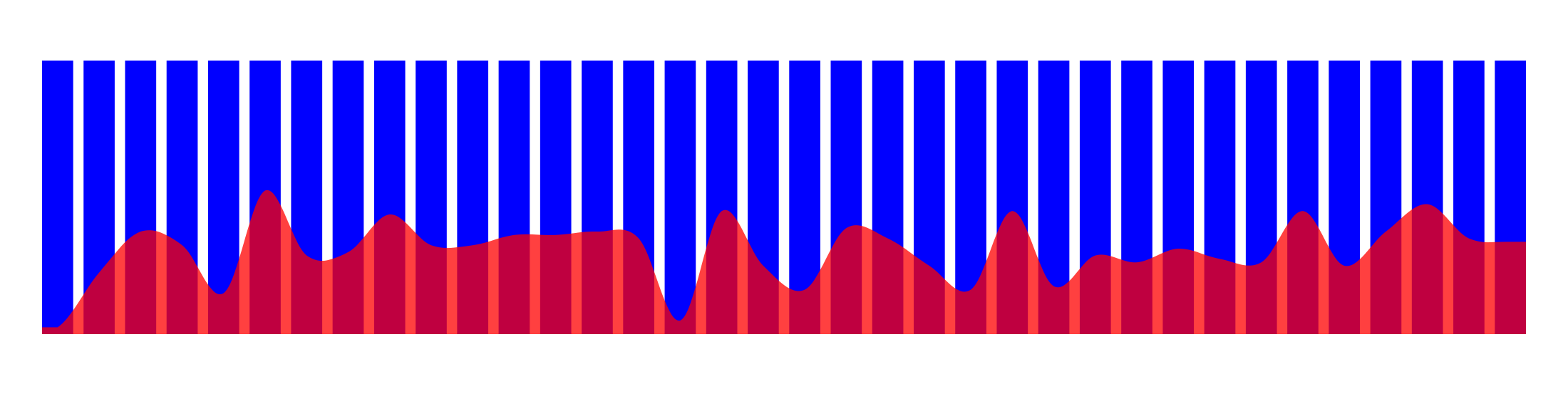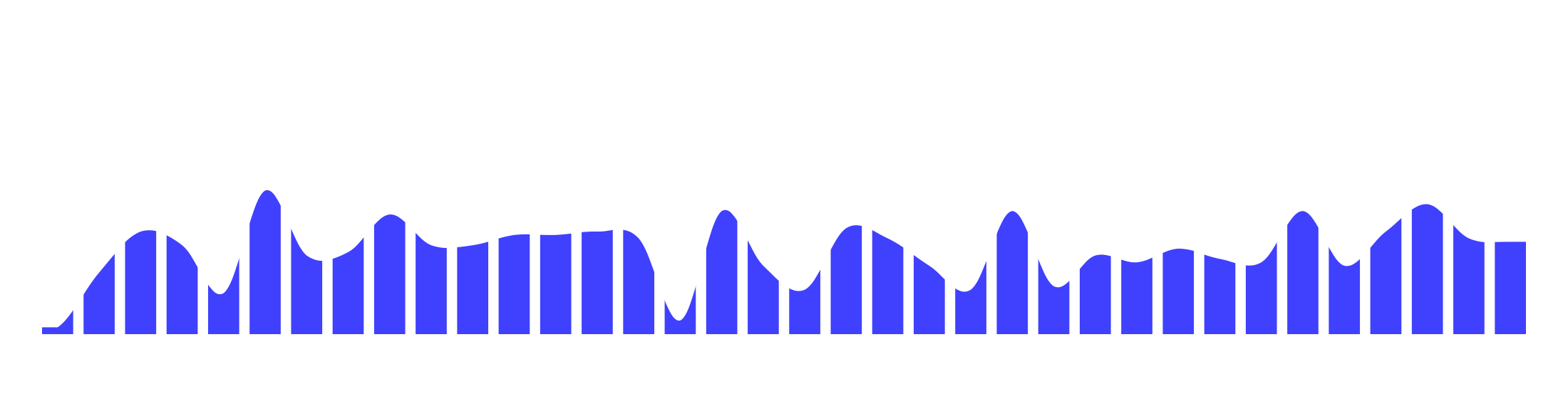
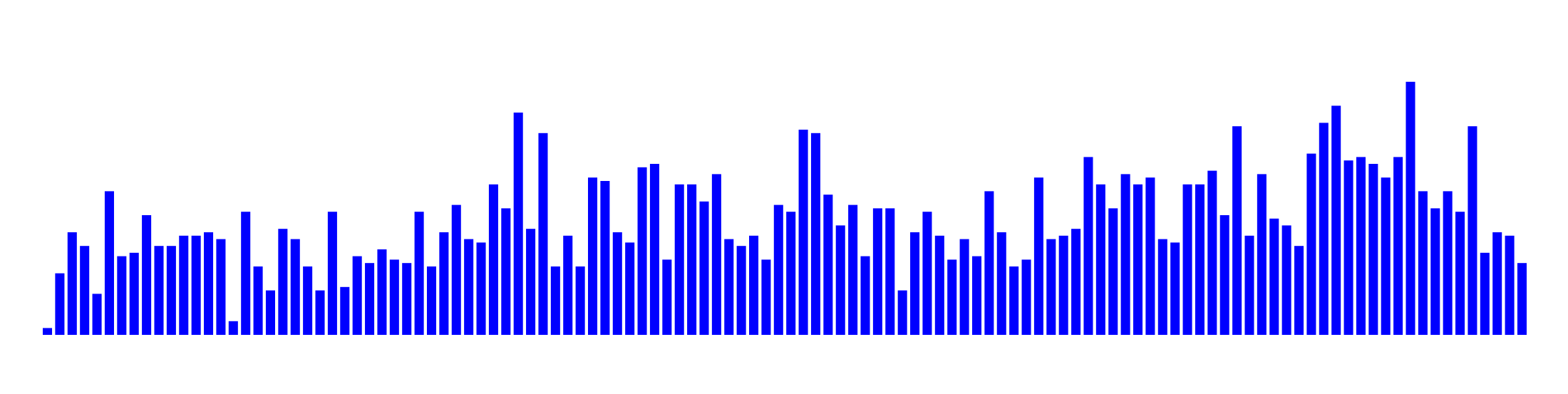
I'm creating an audio waveform, which should look like this:

Notice how the corners of the lines are curved, according to the direction.

My waveform currently has only straight lines:

How can I achieve the desired results?

My current code for the waveform:

fileprivate func createPath(with points: [CGPoint], pointCount: Int, in rect: CGRect) -> CGPath {
    let path = UIBezierPath()
    
    guard pointCount > 0 else {
        return path.cgPath
    }
    
    guard rect.height > 0, rect.width > 0 else {
        return path.cgPath
    }
    
    path.move(to: CGPoint(x: 0, y: 0))
    let minValue = 1 / (rect.height / 2)
    for index in 0..<(pointCount / 2) {
        var point = points[index * 2]
        path.move(to: point)
        point.y = max(point.y, minValue)
        point.y = -point.y
        path.addLine(to: point)
    }
    let scaleX = (rect.width - 1) / CGFloat(pointCount - 1)
    let halfHeight = rect.height / 2
    let scaleY = halfHeight
    var transform = CGAffineTransform(scaleX: scaleX, y: scaleY)
    transform.ty = halfHeight
    path.apply(transform)
    return path.cgPath
}

CodePudding user response：

There are two ways to accomplish this:

1. Rather than treating each bar as a wide line, fill it as a shape, each with its own left, top, right, and bottom. And the top would then be a bézier.

2. Rather than adjust the top of each bar, you can make the bars all go from minimum to maximum values and then add a mask over the whole graph to render the smoothed shape.

   E.g., this shows a few data points, overlays the

Additional observations:

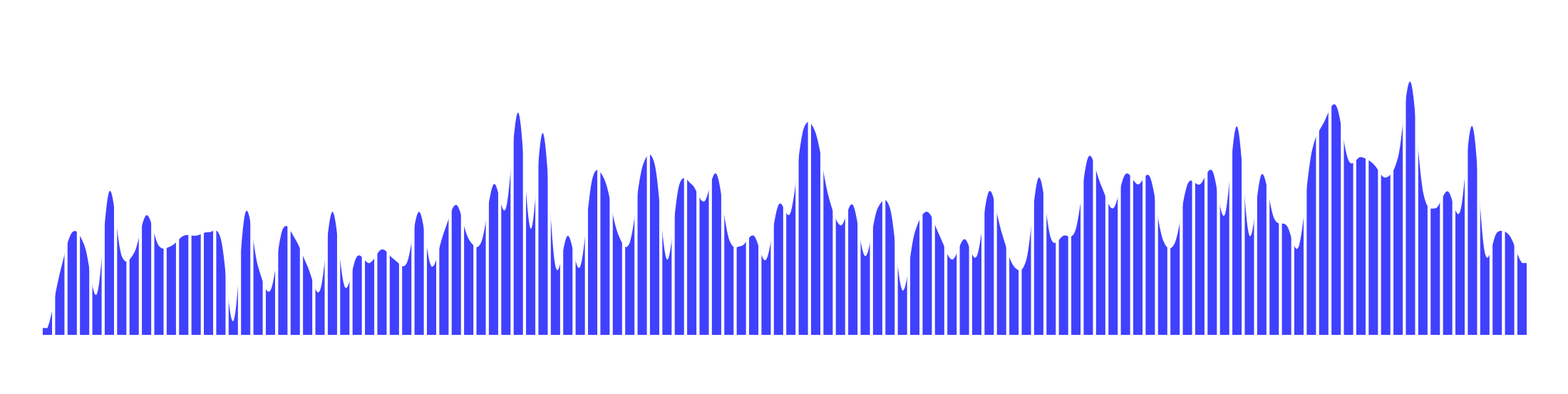
3. Please note, your first image with the curved tops of the bars has another feature that makes it look smooth: The data points, themselves, are smoothed. Your second image features far greater volatility than the first.

   The source of this volatility (which is common in audio tracks, or pretty much any DSP dataset), or lack thereof, is not relevant here. What is relevant is that if the data samples are highly variable, an interpolation algorithm for curving the tops of the bars can actually exaggerate the volatility. Single point spikes will be unusually sharp. Double point spikes will actually appear higher than they really are.

   E.g. consider this dataset:

   

   With something this sort of variability, it could be argued that the “rounding” of the bars makes the results harder to read and/or is misleading:

   

4. While I have attempted to answer the question, one must ask whether this whole exercise is prudent. While there might be an aesthetic appeal to curves to the tops of the bars, it suggests a degree of continuity/precision that is greater than what the underlying data likely supports. The square bars more accurately represent the reality of ranges of values for which data was aggregated and, for this reason, are the common visual representation.