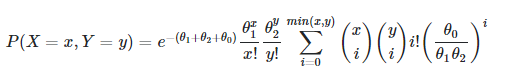Numpy - vectorize the bivariate poisson pmf equation-CodePudding

I'm trying to write a function to evaluate the probability mass function for the bivariate poisson distribution.

This is easy when all of the parameters (x, y, theta1, theta2, theta0) are scalars, but tricky to scale up without loops to allow these parameters to be vectors. I need it to scale such that, for:

theta0 being a scalar - the "correlation parameter" in the equation
theta1 and theta2 having length l
x, y both having length n

the output array would have shape (l, n, n). For example, a slice [j, :, :] from the output array would look like:

The first part (the constant, before the summation) I think i've figured out:

import numpy as np
from scipy.special import factorial

def constant(theta1, theta2, theta0, x, y):

    exponential_part = np.exp(-(theta1   theta2   theta0)).reshape(-1, 1, 1)
    x = np.tile(x, (len(x), 1)).transpose()
    y = np.tile(y, (len(y), 1))

    double_factorial = (np.power(np.array(theta1).reshape(-1, 1, 1), x)/factorial(x)) * \
                       (np.power(np.array(theta2).reshape(-1, 1, 1), y)/factorial(y))

    return exponential_part * double_factorial

But I'm struggling with the summation part. How can I vectorize a summation where the limits depend on variable arrays?

CodePudding user response：

I think I have this figured out, based on the approach that @w-m suggests: calculate every possible summation term which could appear, based on the maximum x or y value which appears, and use a mask to get rid of the ones you don't want. Assuming you have your x and y terms go from 0 to N, in consecutive order, this is calculating up to three times more terms than are actually required, but this is offset by getting to use vectorization.

Reference implementation

I wrote this by first writing a pure-Python reference implementation, which just implements your problem using loops. With 4 nested loops, it's not exactly fast, but it's handy to have while testing the numpy version.

import numpy as np
from scipy.special import factorial, comb
import operator as op
from functools import reduce

def choose(n, r):
    # https://stackoverflow.com/a/4941932/530160
    r = min(r, n-r)
    numer = reduce(op.mul, range(n, n-r, -1), 1)
    denom = reduce(op.mul, range(1, r 1), 1)
    return numer // denom  # or / in Python 2

def reference_impl_constant(s_theta1, s_theta2, s_theta0, s_x, s_y):
    # Cast to float to prevent overflow
    s_theta1 = float(s_theta1)
    s_theta2 = float(s_theta2)
    s_theta0 = float(s_theta0)
    s_x = float(s_x)
    s_y = float(s_y)
    term1 = np.exp(-(s_theta1   s_theta2   s_theta0))
    term2 = (s_theta1 ** s_x / factorial(s_x))
    term3 = (s_theta2 ** s_y / factorial(s_y))
    assert term1 >= 0
    assert term2 >= 0
    assert term3 >= 0
    return term1 * term2 * term3

def reference_impl_constant_loop(theta1, theta2, theta0, x, y):
    theta_len = theta1.shape[0]
    xy_len = x.shape[0]
    constant_array = np.zeros((theta_len, xy_len, xy_len))
    for i in range(theta_len):
        for j in range(xy_len):
            for k in range(xy_len):
                s_theta1 = theta1[i]
                s_theta2 = theta2[i]
                s_theta0 = theta0
                s_x = x[j]
                s_y = y[k]
                constant_term = reference_impl_constant(s_theta1, s_theta2, s_theta0, s_x, s_y)
                assert constant_term >= 0
                constant_array[i, j, k] = constant_term
    return constant_array

def reference_impl_summation(s_theta1, s_theta2, s_theta0, s_x, s_y):
    sum_ = 0
    for i in range(min(s_x, s_y)   1):
        sum_  = choose(s_x, i) * choose(s_y, i) * factorial(i) * ((s_theta0/s_theta1/s_theta2) ** i)
    assert sum_ >= 0
    return sum_

def reference_impl_summation_loop(theta1, theta2, theta0, x, y):
    theta_len = theta1.shape[0]
    xy_len = x.shape[0]
    summation_array = np.zeros((theta_len, xy_len, xy_len))
    for i in range(theta_len):
        for j in range(xy_len):
            for k in range(xy_len):
                s_theta1 = theta1[i]
                s_theta2 = theta2[i]
                s_theta0 = theta0
                s_x = x[j]
                s_y = y[k]
                summation_term = reference_impl_summation(s_theta1, s_theta2, s_theta0, s_x, s_y)
                assert summation_term >= 0
                summation_array[i, j, k] = summation_term
    return summation_array

def reference_impl(theta1, theta2, theta0, x, y):
    # all array inputs must be 1D
    assert len(theta1.shape) == 1
    assert len(theta2.shape) == 1
    assert len(x.shape) == 1
    assert len(y.shape) == 1
    # theta vectors must have same length
    theta_len = theta1.shape[0]
    assert theta2.shape[0] == theta_len
    # x and y must have same length
    xy_len = x.shape[0]
    assert y.shape[0] == xy_len
    # theta0 is scalar
    assert isinstance(theta0, (int, float))
    constant_array = np.zeros((theta_len, xy_len, xy_len))
    output = np.zeros((theta_len, xy_len, xy_len))
    constant_array = reference_impl_constant_loop(theta1, theta2, theta0, x, y)
    summation_array = reference_impl_summation_loop(theta1, theta2, theta0, x, y)
    output = constant_array * summation_array
    return output

Numpy implementation

I split the implementation of this across two functions.

The fast_constant() function calculates everything to the left of the summation symbol. The fast_summation() function calculates everything inside the summation symbol.

import numpy as np
from scipy.special import factorial, comb


def fast_summation(theta1, theta2, theta0, x, y):
    x = np.tile(x, (len(x), 1)).transpose()
    y = np.tile(y, (len(y), 1))
    sum_limit = np.minimum(x, y)
    max_sum_limit = np.max(sum_limit)
    i = np.arange(max_sum_limit   1).reshape(-1, 1, 1)
    summation_mask = (i <= sum_limit)
    theta_ratio = (theta0 / (theta1 * theta2)).reshape(-1, 1, 1, 1)
    theta_to_power = np.power(theta_ratio, i)
    terms = comb(x, i) * comb(y, i) * factorial(i) * theta_to_power
    # mask out terms which aren't part of sum
    terms *= summation_mask
    # axis 0 is theta
    # axis 1 is i
    # axis 2 & 3 are x and y
    # so sum across axis 1
    terms = terms.sum(axis=1)
    
    return terms

def fast_constant(theta1, theta2, theta0, x, y):
    theta1 = theta1.astype('float64')
    theta2 = theta2.astype('float64')
    exponential_part = np.exp(-(theta1   theta2   theta0)).reshape(-1, 1, 1)
    # x and y must be 1D
    assert len(x.shape) == 1
    assert len(y.shape) == 1
    # x and y must have same shape
    assert x.shape == y.shape
    x_len, y_len = x.shape[0], y.shape[0]
    x = x.reshape((x_len, 1))
    y = y.reshape((1, y_len))

    double_factorial = (np.power(np.array(theta1).reshape(-1, 1, 1), x)/factorial(x)) * \
                       (np.power(np.array(theta2).reshape(-1, 1, 1), y)/factorial(y))

    return exponential_part * double_factorial

def fast_impl(theta1, theta2, theta0, x, y):
    return fast_summation(theta1, theta2, theta0, x, y) * fast_constant(theta1, theta2, theta0, x, y)

Benchmarking

Assuming that X and Y range from 0 to 20, and that theta is centered somewhere inside that range, I get the result that the numpy version is roughly 280 times faster than the pure python reference.

Numerical stability

I'm unsure how numerically stable this is. For example, when I center theta at 100, I get a floating-point overflow. Typically, when computing an expression which has lots of choose and factorial expressions inside it, you'll use some mathematical equivalent which results in smaller intermediate sums. In this case I have so little understanding of the math that I don't know how you'd do that.